Derivatives
The derivative \(r'\) of a vector function \(r\) is
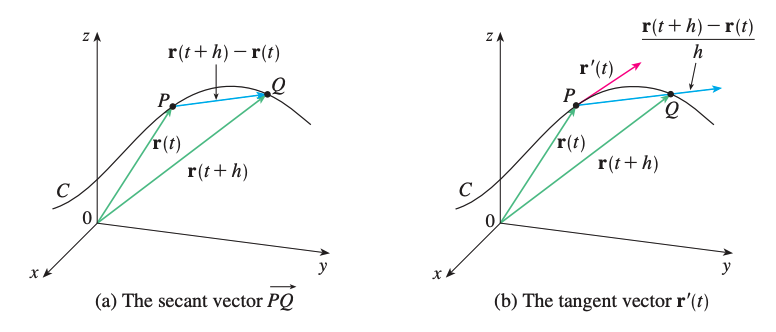
\[\frac{dr}{dt}=r'(t)=\lim\_{h \rightarrow 0}\frac{r(t+h)-r(t)}{h}\]If the points \(P\) and \(Q\) have position vectors \(r(t)\) and \(r(t+h)\), then \(\vec{PQ}\) represents the secant vector \(r(t+h)-r(t)\). As \(h \rightarrow 0\), \(\vec{PQ}\) approaches the tangent vector.
We define \(r'(t)\) as the tangent vector to the curve defined by \(r\) at the point \(P\), provided that \(r'(t)\) exists and \(r'(t) \neq 0\).
The line \(L\) through \(P\) and parallel to \(r'(t)\) is called the tangent line to \(C\) at \(P\).
Unit Tangent Vector
The unit tangent vector is defined as
\[T(t) = \frac{r'(t)}{\lvert r'(t) \rvert}\]Derivative of r(t)
If \(r(t) = \left\langle f(t), g(t), h(t), \right\rangle\), where \(f, g, h\) are differentiable functions, then
\[r'(t) = \left\langle f'(t), g'(t), h'(t) \right\rangle\][Note] Just as for real-valued functions, the second derivative is defined in the similar way.
Differentiation Rules
Suppose \(u\) and \(v\) are differentiable vector functions, \(c\) is a scalar, and \(f\) is a real-valued function. Then,
[1] \(\frac{d}{dt} [u(t) + v(t)] = u'(t) + v'(t)\)
[2] \(\frac{d}{dt}[cu(t)] = cu'(t)\)
[3] \(\frac{d}{dt} [f(t)u(t)] = f'(t)u(t) + f(t)u'(t)\)
[4] \(\frac{d}{dt}[u(t) \cdot v(t)] = u'(t) \cdot v(t) + u(t) \cdot v'(t)\)
[5] \(\frac{d}{dt}[u(t) \times v(t)]=u'(t) \times v(t) + u(t) \times v'(t)\)
[6] \(\frac{d}{dt}[u(f(t))] = f'(t)u'(f(t))\)
example 1
Show if \(\lvert r(t) \rvert = c\), then \(r'(t)\) is orthogonal to \(r(t)\) for all \(t\).
Since \(r(t) \cdot r(t) = c^2\), \(r'(t)r(t)+r(t)r'(t)=0\)
Hence, \(r'(t) \cdot r(t) = 0\). Since the dot product is \(0\), they’re orthogonal.
Integrals
The definite integral of a continuous vector function \(r(t)\) is defined as
\[\int_a^b r(t)dt = \left\langle \int_a^b f(t)dt, \int_a^b g(t)dt, \int_a^b h(t)dt \right\rangle\]where \(f, g, h\) are component functions.
In other words, we simply evaluate an integral for each component function to get the integral of the whole vector function.
With the Fundamental Theorem of Calculus, we get
\[\sum_a^b r(t)dt = R(b) - R(a)\]where \(R\) is an antiderivative of \(r\): \(R'(t)=r(t)\). Also, we use the notation \(\int r(t)dt\) for indefinite integrals (antiderivatives).
Exercises
Q10
Find the derivative of the vector function \(r(t) = \left\langle e^{-t}, t-t^3, \ln t \right\rangle\).
\[r'(t) = \left\langle -e^{-t}, 1-3t^2, \frac{1}{t} \right\rangle\]Q15
Find the derivative of the vector function \(r(t) = \vec{a} + t\vec{b} + t^2\vec{c}\).
Notice that \(\vec{a}, \vec{b}, \vec{c}\) are not vector functions but just vectors so we must treat them as constants.
\[r'(t) = \vec{b} + 2t\vec{c}\]Q19
Find the unit tangent vector \(T(t)\) at the point with the given value of the parameter \(t\): \(r(t) = \cos{t} \vec{i} + 3t \vec{j} + 2 \sin{2t} \vec{k}\)
Let’s first find \(r'(t)\)
\[r'(t) = \left\langle -\sin{t}, 3, 4\cos{2t} \right\rangle\] \[r'(0) = \left\langle 0, 3, 4 \right\rangle\]From the definition of unit tangent vector \(T(t) = \frac{r'(t)}{\lvert r'(t) \rvert}\),
\[\lvert r'(t) \rvert = \sqrt{\sin^2t+9+16\cos^2{2t}}\] \[\lvert r'(0) \rvert = 5\]Hence,
\[\frac{r'(0)}{\lvert r'(0) \rvert} = \left\langle 0, \frac{3}{5}, \frac{4}{5} \right\rangle\]Q25
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point.
\[x=e^{-t}\cos{t},\ y=e^{-t} \sin{t},\ z=e^{-t},\ (1,0,1)\]We observe that the \(t\) that satisfies the given equation is \(t=0\).
Let \(r(t) = \left\langle e^{-t}\cos{t},\ e^{-t} \sin{t},\ e^{-t} \right\rangle\). Then,
\[r'(t) = \left\langle -e^{-t}\cos{t} - e^{-t}\sin{t},\ -e^{-t}\sin{t}+e^{-t}\cos{t},\ -e^{-t} \right\rangle\] \[r'(0) = \left\langle -1, 1, -1 \right\rangle\]Therefore, the tangent vector is \(\left\langle -1, 1, -1 \right\rangle\) at \(t=0\).
Hence, the equation of the tangent line that goes through the point \((1, 0, 1)\) to the curve is
\[\left\langle 1, 0, 1\right\rangle + t \left\langle -1, 1, -1 \right\rangle\]Hence,
\[x = 1-t\] \[y=t\] \[z=1-t\]Q37
Evaluate the integral
\[\int_0^1 \left( \frac{1}{t+1}\vec{i} + \frac{1}{t^2+1}\vec{j}+\frac{t}{t^2+1}\vec{k} \right)dt\]We evaulate integral for each component function.
\[(\text{substitute}\ u=t+1)\ \int_0^1 \frac{1}{t+1}dt = \int_1^2 \frac{1}{u}du = \ln 2-\ln 1=\ln2\] \[\int_0^1 \frac{1}{t^2+1}dt = tan^{-1}1 - tan^{-1}0 = \frac{\pi}{4}\] \[(\text{substitute}\ u=t^2+1)\ \int_0^1 \frac{t}{t^2+1}dt = \frac{1}{2}\int_1^2 \frac{1}{u}du = \frac{\ln2}{2}\] \[\therefore \left\langle \ln2, \frac{\pi}{4}, \frac{\ln2}{2} \right\rangle\]Q55
If \(r(t) \neq \vec{0}\), show that \(\frac{d}{dt} \lvert r(t) \rvert = \frac{1}{\lvert r(t) \rvert} r(t) \cdot r'(t)\).
\[\frac{d}{dt} \lvert r(t) \rvert = \frac{d}{dt} \sqrt{r(t) \cdot r(t)}\] \[= \frac{1}{2 \sqrt{r(t) \cdot r(t)}} 2r(t) \cdot r'(t)\ \cdots \text{chain rule}\] \[= \frac{1}{\sqrt{r(t) \cdot r(t)}} r(t) \cdot r'(t)\] \[= \frac{1}{\lvert r(t) \rvert} r(t) \cdot r'(t)\]References
[1] Stewart Calculus 8th Edition