Length of a Curve
Suppose a curve has the vector equation \(r(t) = \left\langle f(t), g(t), h(t) \right\rangle,\ a \leq t \leq b\), or, equivalently, the parametric equations \(x=f(t), y=g(t), z=h(t)\) where \(f', g', h'\) are continuous. Also, if the curve is traversed exactly one as \(t\) increases from \(a\) to \(b\), then its length is
\[L = \int_a^b{\sqrt{f'(t)^2+g'(t)^2+h'(t)^2}}dt\] \[= \int_a^b \sqrt{ \left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 + \left(\frac{dz}{dt}\right)^2} dt\] \[= \int_a^b \lvert r'(t) \rvert dt\]Arc Length Function
Suppose that \(C\) is a curve given by a vector function
\[r(t) = \left\langle f(t), g(t), h(t) \right\rangle,\ a \leq t \leq b\]where \(r'\) is continuous and \(C\) is traversed exactly once as \(t\) increases from \(a\) to \(b\). Then, the arg length function \(s\) is defined by
\[s(t) = \int_a^t \lvert r'(u) \rvert du\]\(s(t)\) is the length of the part of \(C\) between \(r(a)\) and \(r(t)\). Using the Fundamental Theorem of Calculus, we get
\[\frac{ds}{dt} = \lvert r'(t) \rvert\]It’s often useful to parametrize a curve w.r.t arc length instead of \(t\). With \(r(t)\) and \(s(t)\), we may be able to solve for \(t\) as a function of \(s\): \(t = t(s)\). Then, \(C\) can be reparametrized in terms of \(s\) by substituting for \(t\): \(r = r(t(s))\) .
example
Reparametrize \(r(t) = \left\langle \cos{t}, \sin{t}, t \right\rangle\) w.r.t arc length measured from \((1,0,0)\) in the direction of increasing \(t\).
We know that the initial point \((1,0,0)\) is given when \(t=0\).
Also, \(r'(t) = \left\langle -\sin{t}, \cos{t}, 1 \right\rangle\).
The arc length function is then \(S=s(t)=\int_0^t \lvert r'(u) \rvert du = \int_0^t \sqrt{2} du = \sqrt{2}t\)
Then we can express \(t\) in terms of \(s\): \(t = \frac{s(t)}{\sqrt{2}}\).
Let’s substitute \(r(t)\) with \(r(\frac{s(t)}{\sqrt{2}})\)
\[r(t) = r \left( \frac{s(t)}{\sqrt{2}} \right) = \left\langle \cos \left( {\frac{s(t)}{\sqrt{2}}} \right), \sin \left( {\frac{s(t)}{\sqrt{2}}} \right), \left( \frac{s(t)}{\sqrt{2}} \right) \right\rangle\]Curvature
A parametrization \(r(t)\) is called smooth on an interval \(I\) if \(r'\) is continuous and \(r'(t) \neq 0\) on \(I\). A curve is called smooth if it has a smooth parametrization. A smooth curve has no sharp corners or cusps.
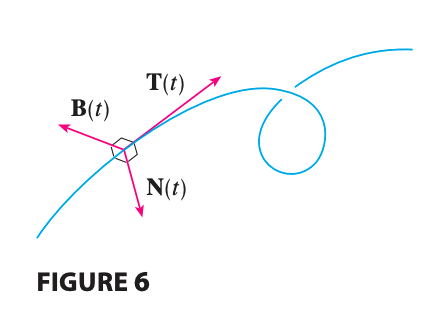
If \(C\) is a smooth curve \(r(t)\), the unit tangent vector \(T(t)\) is given by
\[T(t) = \frac{r'(t)}{\lvert r'(t) \rvert}\]and indicates the direction of the curve.
The curvature of \(C\) at a given point is a measure of how quickly the curve changes direction at that point. Specifically, it’s defined as the magnitude of the rate of change of the unit tangent vector w.r.t arc length. Since the unit tangent vector has constant length, only directional changes contribute to the rate of change of \(T\).
The curvature of a curve is \(K = \left\lvert \frac{dT}{ds} \right\rvert\)
where \(T\) is the unit tangent vector.
Also, the curvature is easier to compute if it’s expressed in terms of \(t\) instead of \(s\).
Since \(\frac{dT}{dt}=\frac{dT}{ds} \frac{ds}{dt}\),
\[K = \left\lvert \frac{dT}{ds} \right\rvert = \left\lvert \frac{dT/dt}{ds/dt} \right\rvert\]and \(\frac{ds}{dt} = \lvert r'(t) rvert\), we can parametrize the curvature w.r.t \(t\):
\[k(t) = \frac{\lvert T'(t) \rvert}{\lvert r'(t) \rvert}\]Alternative vector function for the curvature is
\[k(t) = \frac{\lvert r'(t) \times r''(t) \rvert}{\lvert r'(t) \rvert^3}\]Normal and Binormal vectors
Unit Normal vector
At a given point on a smooth space curve \(r(t)\), there’re many vectors that are orthogonal to \(T(t)\). We’re insterested in one such vector. Since \(\lvert T(t) \rvert = 1\) for all \(t\), we have \(T(t) \cdot T'(t) = 0\). Hence \(T'(t)\) is orthogonal to \(T(t)\).
We define the principal unit normal vector or unit normal \(N(t)\) as
\(N(t) = \frac{T'(t)}{\lvert T'(t) \rvert}\).
We can interpret \(N(t)\) as the direction in which the curve is turning at each point.
Binormal vector
A vector perpendicular to both \(T\) and \(N\) is called the binormal vector and defined as
\[B(t) = T(t) \times N(t)\]and \(B\) is also a unit vector.
Normal and Osculating Plane
Normal Plane
The plane determined by the normal and binormal vectors \(N\) and \(B\) at a point \(P\) on \(C\) is called the normal plane of \(C\) at \(P\). The normal plane consists of all lines orthogonal to the tangent vector \(T\).
Osculating Plane
The plane determined by the vectors \(T\) and \(N\) is called the osculating plane of \(C\) at \(P\). It’s a plane that comes closest to containing the part of the curve near \(P\).
Formula Summary
Arc Length
\[L = \int_a^b \lvert r'(t) \rvert dt\] \[s(t) = \int_a^t \lvert r'(u) \rvert du\] \[\frac{ds}{dt} = \lvert r'(t) \rvert\]Curvature
\[T(t) = \frac{r'(t)}{\lvert r'(t) \rvert}\] \[N(t) = \frac{T'(t)}{\lvert T'(t) \rvert}\] \[B(t) = T(t) \times N(t)\] \[K = \left\lvert \frac{dT}{ds} \right\rvert = \frac{\lvert T'(t) \rvert}{\lvert r'(t) \rvert} = \frac{\lvert r'(t) \times r''(t) \rvert}{\lvert r'(t) \rvert^3}\]References
[1] Stewart Calculus 8th Edition