Functions of Two Variables
A function \(f\) of two variables is a rule that assigns each ordered pair of real numbers \((x,y)\) in a set \(D\) to a unique real number denoted by \(f(x,y)\). The set \(D\) is the domain of \(f\) and its range is the set of values that \(f\) takes on: \(\{f(x,y) \lvert (x,y) \in D\}\).
We often write it as \(z=f(x,y)\). The variables \(x\) and \(y\) are independent variables and \(z\) is the dependent variable.
Graphs
Graph is a way of visualizing the behavior of a function of two variables.
If \(f\) is a function of two variables with domain \(D\), then the graph of \(f\) is the set of all points \((x,y,z)\) in \(\mathbb{R}^3\) such that \(z=f(x,y)\) and \((x,y)\) is in \(D\)
 |
|---|
| stewart-calculus-8th-edition |
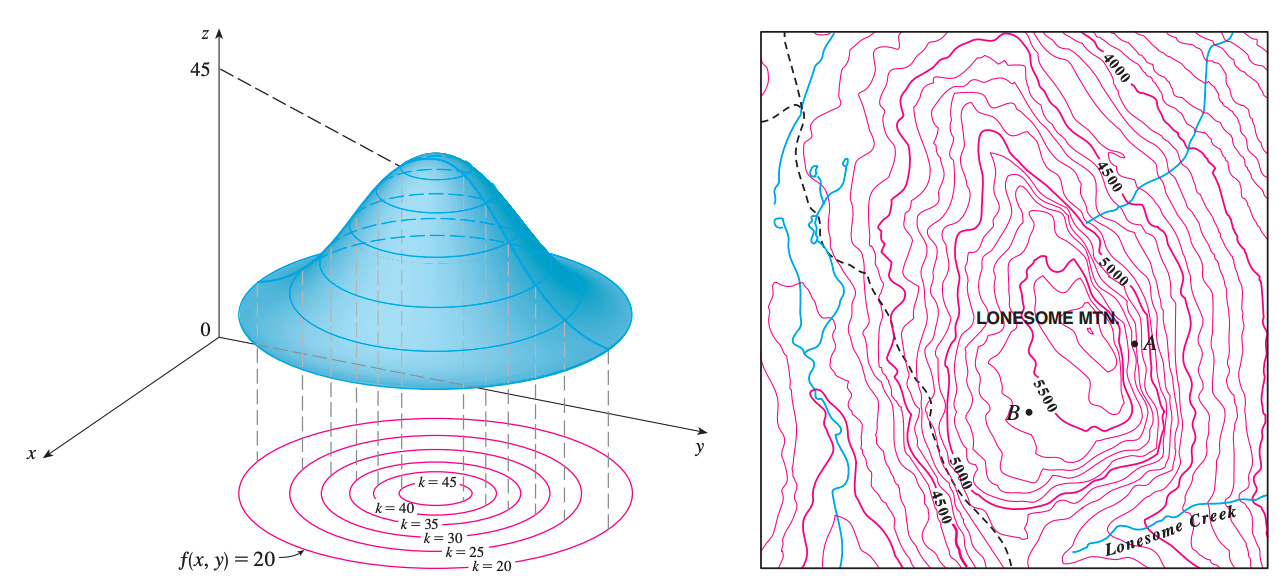
Level Curves
The level curves of a function \(f\) of two variables are the curves with equations \(f(x,y)=k\), where \(k\) is a constant (in the range of \(f\)).
 |
|---|
| stewart-calculus-8th-edition |
References
[1] Stewart Calculus 8th Edition