Tangent Planes
 |
|---|
| stewart-calculus-8th-edition |
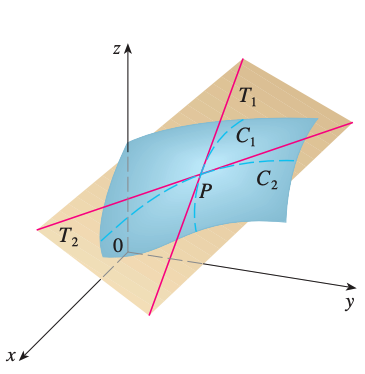
Suppose a surface \(S\) has equation \(z=f(x,y)\) where \(f\) has continuous first partial derivatives. Let \(P(x_0,y_0,z_0)\) be a point on \(S\). Also, let \(C_1\) and \(C_2\) be the curves obtained by intersecting the vertical planes \(y=y_0\) and \(x=x_0\) with the surface \(S\) as shown in the figure above. Then, the point \(P\) lies on both \(C_1\) and \(C_2\).
Let \(T_1\) and \(T_2\) be the tangent lines to the curves \(C_1\) and \(C_2\) at \(P\). Then, the tangent plane to the surface \(S\) at the point \(P\) is the plane that contains both tangent lines \(T_1\) and \(T_2\).
It can be shown that the tangent line of any other curce \(c\) that lines on the surface \(S\) passing through \(P\) also lies in the tangent plane. Hence, the tangent plane to \(S\) at \(P\) can be interpreted as the plane consisting of all possible tangent lines at \(P\) to curves that lie on \(S\) passing through \(P\). The tangent plane at \(P\) is the plane that most closely approximates the surface \(S\) near the point \(P\).
The equation for any plan passing through \(P(x_0, y_0, z_0)\) is
\[A(x-x_0)+B(y-y_0)+C(z-z_0) = 0\]Divide it by \(C\),
\[\frac{A}{C}(x-x_0)+\frac{B}{C}(y-y_0)+(z-z_0) = 0\] \[(z-z_0) = -\frac{A}{C}(x-x_0) - \frac{B}{C}(y-y_0)\]Let \(a = -A/C\) and \(b = -B/C\)
\[(z-z_0) = a(x-x_0) + b(y-y_0)\]If this represents the tangent plane at \(P\), then its intersection with the plane \(y=y_0\) must be the tangent line \(T_1\). Hence, we set \(y=y_0\) and it gives
\[(z-z_0) = a(x-x_0)\ \text{ where } y=y_0\]This is the point-slope equation of a line with slope \(a\). But we know that the slop of the tangent \(T_1\) is \(f_x(x_0,y_0)\). Therefore, \(a = f_x(x_0,y_0)\).
If we operate the same procedure for \(x=x_0\), we get
\[(z-z_0) = b(y-y_0)\ \text{ where } x=x_0\]where \(b=f_y(x_0,y_0)\)
Finally we can define the equation of the tangent plane.
Tangent Plane Equation
\[z-z_0 = f_x(x_0,y_0)(x-x_0) + f_y(x_0,y_0)(y-y_0)\]Suppose \(f\) has continuous partial derivatives. An equation of the tangent plane to the surface \(z=f(x,y)\) at the point \(P(x_0, y_0, z_0)\) is
or
\[z = f(a,b) + f_x(x_0,y_0)(x-x_0) + f_y(x_0,y_0)(y-y_0)\]Example
Find the tangent plane to the elliptic paraboloid \(z=2x^2+y^2\) at the point \((1,1,3)\)
Let \(f(x,y) = 2x^2+y^2\). The tangent plane equation is given by \(z-z_0 = f_x(x_0,y_0)(x-x_0) + f_y(x_0,y_0)(y-y_0)\).
\[f_x(x,y) = 4x\] \[f_y(x,y) = 2y\]Hence, at \((1,1,3)\),
\[f_x(1,1) = 4\] \[f_y(1,1) = 2\] \[z-3 = 4(x-1) + 2(y-1)\] \[\therefore z = 4x+2y-3\]Linear Approximations
In the above example, we found the tangent plane to the graph of the function \(f(x,y) = 2x^2 + y^2\). This tangent plane is a good approximation to \(f(x,y)\) when \((x,y)\) is near \((1,1)\). The function \(L\) is called the linearization of \(f\) at \((1,1)\) and the approximation
\[f(x,y) \approx 4x + 2y - 3\]is called the linear approximation or tangent plane approximation of \(f\) at \((1,1)\).
In general, the tangent plane to \(f\) (two variables) at \((a, b, f(a,b))\) is
\[z = f(a,b) + f_x(a,b)(x-a) + f_y(a,b)(y-b)\]Then, we can define linearization and linear approximation
Linearization
\[L(x,y) = f(a,b) + f_x(a,b)(x-a) + f_y(a,b)(y-b)\]is called the linearization of \(f\) at \((a,b)\)
Linear approximation
\[f(x,y) \approx f(a,b) + f_x(a,b)(x-a) + f_y(a,b)(y-b)\]is called the linear approximation or the tangent plane approximation of \(f\) at \((a,b)\).
Differentiable
We previously defined tangent plane where \(f\) has continuous first partial derivatives. But if \(f_x\) and \(f_y\) are not continuous?, we might get a bad approximation. To rule out such behavior, we formulate the idea of differentiable function of two variables.
Consider a function of two variables \(z = f(x,y)\) and suppose \(x\) changes from \(a\) to \(a + \Delta x\) and \(y\) changes from \(b\) to \(b + \Delta y\). THen, the corresponding increment of \(z\) is
\[\Delta z = f(a + \Delta x, b + \Delta y) - f(a,b)\]From this, formulate the definition:
Definition
If \(z=f(x,y)\), then \(f\) is differentiable at \((a,b)\) if \(\Delta z\) can be expressed in the form
\[\Delta z = f_x(a,b)\Delta x + f_y(a,b) \Delta + \epsilon_1 \Delta x + \epsilon_2 \Delta y\]where \(\epsilon_1, \epsilon_2 \rightarrow 0\) as \((\Delta x, \Delta y) \rightarrow (0,0)\)
A differentiable function is one for which the linear approximation is a good approximation.
Alternative Definition
It’s sometimes hard to use the above definition to check differentiablity. The following theorem provides a simpler but sufficient condition for differentiability
If the partial derivatives \(f_x\) and \(f_y\) exist near \((a,b)\) and are continuous at \((a,b)\), then \(f\) is differentiable at \((a,b)\).
Differentials
 |
|---|
| single variable (stewart-calculus-8th-edition) |
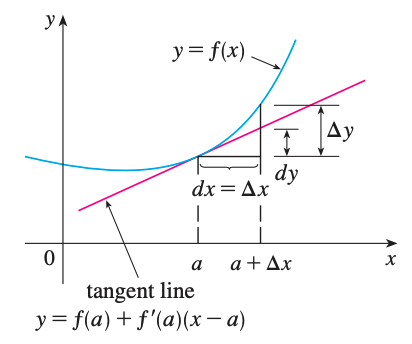
For a differentiable univariate function \(y=f(x)\), the differential \(dx\) is an independent variable; that is, \(dx\) can be given any real number. The differential of \(y\) is then defined as
\[dy = f'(x)dx\][1] \(\Delta y\) - change in height of \(y=f(x)\)
[2] \(dy\) - changed in height of the tangent line when \(x\) changes by an amount \(dx = \Delta x\)
 |
|---|
| stewart-calculus-8th-edition |
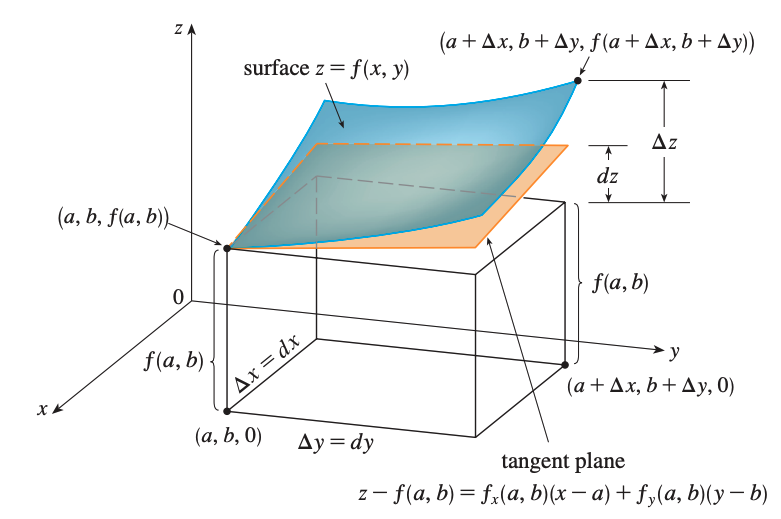
For a differentiable function with two variables, \(z = f(x,y)\), we define the differentials \(dx\) and \(dy\) to be independent variables (any values). Then, the differential \(dz\), also called the total differential, is defined by
\[dz = f_x(x,y)dx + f_y(x,y)dy\] \[= \frac{\partial z}{\partial x}dx + \frac{\partial z}{\partial y}dy\]If we take \(dx = \Delta x = x - a\) and \(dy = \Delta y = y - b\) in the above equation, then the differential of \(z\) is
\[dz = f_x(a,b)(x-a) + f_y(a,b)(y-b)\]So, we can rewrite the linear approximation using differential:
\[f(x,y) \approx f(a,b) + dx\]References
[1] Stewart Calculus, 8th edition