The Chain Rule
Single Variable
The chain rule for a single variable gives the rule for differentiating a composite function: If \(y=f(x)\) and \(x=g(t)\), where \(f\) and \(g\) are differentiable functions: \(y=f(g(t))\)
\[\frac{dy}{dt} = \frac{dy}{dx} \frac{dx}{dt}\]or
\[y = f'(g(t)) \cdot g'(t)\][Chain Rule] Multi-variable: Case 1
Suppose that \(z = f(x,y)\) is a differentiable function of \(x\) and \(y\), where \(x = g(t)\) and \(y = h(t)\) are both differentiable functions of \(t\). Then, \(z\) is a differentiable function of \(t\) and
\[\frac{dz}{dt} = \frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt}\]Since we often write \(\partial z / \partial x\) as \(\partial f / \partial x\), we can rewrite the chain rule as
\[\frac{dz}{dt} = \frac{\partial z}{\partial x}\frac{dx}{dt} + \frac{\partial z}{\partial y}\frac{dy}{dt}\]Example 1
\(z = x^2y + 3xy^4\) where \(x=\sin{2t}\) and \(y=\cos{t}\). Find \(dz/dt\) when \(t = 0\)
\[\frac{\partial z}{\partial x} = 2xy + 3y^4,\ \ \frac{dx}{dt} = 2 \cos{2t}\] \[\frac{\partial z}{\partial y} = x^2 + 12xy^3,\ \ \frac{dy}{dt} = -\sin{t}\]Hence,
\[\frac{dz}{dt} = (2xy+3y^4)(2\cos{2t}) + (x^2 + 12xy^3)(-\sin{t})\]Since \(x=0\) and \(y=1\) when \(t=0\),
\[\frac{dz}{dt} \bigg\vert\_{t=0} = 6\][Chain Rule] Multi-variable: Case 2
Suppose \(z = f(x,y)\) is a differentiable function of \(x\) and \(y\), where \(x = g(s,t)\) and \(y=h(s,t)\) are differentiable functions of \(s\) and \(t\). Then,
\[\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial s} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial s}\] \[\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial t}\]Independent, Intermediate, Dependent Variables
For Case 2 of the chain rule,
[1] \(s\) and \(t\) are independent variables
[2] \(x\) and \(y\) are intermediate variables
[3] \(z\) is the dependent variable
Example 3
If \(z = e^x\sin{y}\) where \(x = st^2\) and \(y=s^2t\), find \(\partial z/ \partial s\) and \(\partial z / \partial t\).
\[\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial s} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial s} = (e^x \sin{y})(t^2) + (e^x \cos{y})(2st)\] \[\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial t} = (e^x\sin{y})(2st) + (e^x\cos{y})(s^2)\][Chain Rule] Multi-variable: General Version
Suppose that \(u\) is a differentiable function of \(n\) variables \(x_1,x_2,...,x_n\) and each \(x_j\) is a differentiable function of the \(m\) variables \(t_1,t_2,...,t_m\). Then \(u\) is a function of \(t_1, t_2,...,t_m\) and
\[\frac{\partial u}{\partial t_i} = \frac{\partial u}{\partial x_i}\frac{\partial x_i}{\partial t_i} + \frac{\partial u}{\partial x_2}\frac{\partial x_2}{\partial t_i}+ \cdots + \frac{\partial u}{\partial x_n}\frac{\partial x_n}{\partial t_i}\]for each \(i=1,2,...,m\)
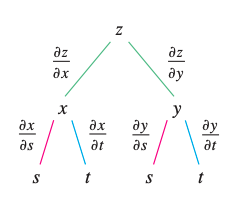
Tree Diagram
It’s often useful to draw tree diagram to visualize the chain rule. Let’s take Case 2.
\[\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial s} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial s}\] \[\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial t}\]Then, the tree diagram can be drawn as follow,
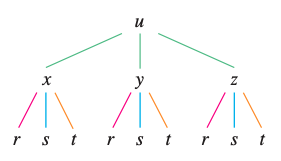
Example 5
If
\[u = x^4y + y^2z^3\] \[x=rse^t\] \[y=rs^2e^{-t}\] \[z=r^2s \sin{t}\]then the tree diagram is
If we want to find, for example, \(\frac{\partial u}{\partial s}\), then add all the “routes” from \(u\) to \(s\).
\[\frac{\partial u}{\partial s} = \frac{\partial u}{\partial x}\frac{\partial x}{\partial s} + \frac{\partial u}{\partial y}\frac{\partial y}{\partial s} + \frac{\partial u}{\partial z}\frac{\partial z}{\partial s}\]Implicit Differentiation: Case 1
The Chain Rule can be used for implicit differentiation.
Suppose \(F(x,y)=0\) defines \(y\) implicitly as a differentiable function of \(x\), that is, \(y=f(x)\), where \(F(x, f(x))= 0\) for all \(x\) in the domain of \(f\). If \(F\) is differentiable, we can apply Case 1 Chain rule to differentiate both sides of \(F(x,y) = 0\) w.r.t \(x\).
\[\frac{\partial F}{\partial x}\frac{\partial x}{\partial x} + \frac{\partial F}{\partial y}\frac{\partial y}{\partial x} = 0\]If \(\partial F / \partial y \neq 0\), then we can solve for \(dy/dx\):
\[\frac{dy}{dx} = -\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} = -\frac{F_x}{F_y}\]To derive this equation, we assumed that \(F(x,y)=0\) defines \(y\) implicitly as a function of \(x\).
Example 8
Q) Find \(y'\) if \(x^3 + y^3 = 6xy\)
We can wewrite it as
\[F(x,y) = x^3 + y^3 - 6xy = 0\]Using the equation above,
\[\frac{dy}{dx} = -\frac{F_x}{F_y} = -\frac{3x^2-6y}{3y^2-6x} = -\frac{x^2 - 2y}{y^2 - 2x}\]Implicit Differentiation: Case 2
Now suppose that \(z\) is given implicitly as a function of \(z=f(x,y)\) by an equation of \(F(x,y,z) = 0\). This means that \(F(x,y,f(x,y))=0\) for all \((x,y)\) in the domain of \(f\). If \(F\) and \(f\) are differentiable, then we can differentiate \(F(x,y,z)\) w.r.t \(x\) as follows:
\[\frac{\partial F}{\partial x}\frac{\partial x}{\partial x} + \frac{\partial F}{\partial y}\frac{\partial y}{\partial x} + \frac{\partial F}{\partial z}\frac{\partial z}{\partial x} = 0\]But
\[\frac{\partial}{\partial x} (x) = 1,\ \ \frac{\partial}{\partial x}(y) = 0\]Hence, it becomes
\[\frac{\partial F}{\partial x} + \frac{\partial F}{\partial z}\frac{\partial z}{\partial x} = 0\]If \(\partial F / \partial z \neq 0\), we solve for \(\partial z / \partial x\):
\[\frac{\partial z}{\partial x}=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}} = -\frac{F_x}{F_z}\] \[\frac{\partial z}{\partial y}=-\frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial z}} = -\frac{F_y}{F_z}\]Example 8
Find \(\frac{\partial z}{\partial x}\) and \(\frac{\partial z}{\partial y}\) if \(x^3+y^3+z^3+6xyz = 1\).
Let \(F(x,y,z) = x^3+y^3+z^3+6xyz - 1 = 0\)
Then we can use the equatio:
\[\frac{\partial z}{\partial x} = -\frac{F_x}{F_z} = -\frac{2x^2+6yz}{3z^2+6xy} = -\frac{x^2 + 2yx}{z^2 + 2xy}\] \[\frac{\partial z}{\partial y} = -\frac{F_x}{F_z} = -\frac{2y^2+6xz}{3z^2+6xy} = -\frac{y^2 + 2xz}{z^2 + 2xy}\]References
[1] Stewart Calculus, 8th edition