Directional Derivatives
Recall that if \(z = f(x,y)\), then the partial derivatives \(f_x\) and \(f_y\) are
\[f*x(x_0, y_0) = \lim*{h \rightarrow 0} \frac{f(x_0 + h, y_0) - f(x_0, y_0)}{h}\] \[f*y(x_0, y_0) = \lim*{h \rightarrow 0} \frac{f(x_0, y_0 + h) - f(x_0, y_0)}{h}\]But what if we want to find the rate of change of \(z\) at \((x_0, y_0)\) in the direction of an arbitrary unit vector \(u = \left\langle a, b \right\rangle\)?
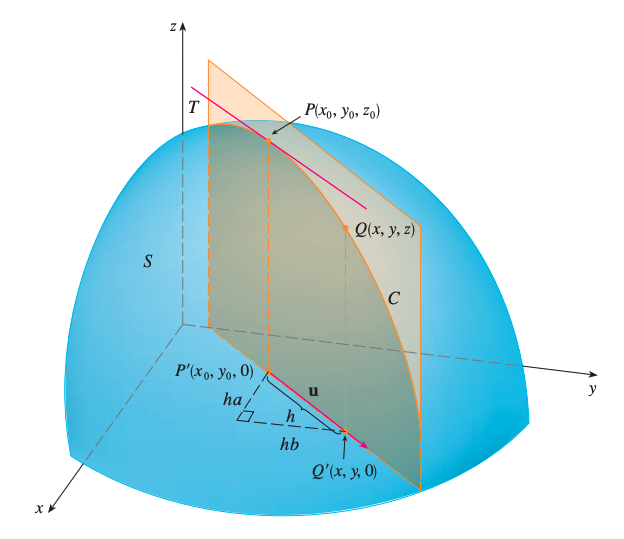
We consider the surface \(S\) with the equation \(z = f(x,y)\) and we let \(z_0 = f(x_0, y_0)\). Then, \(P(x_0, y_0, z_0)\) lies on \(S\). The vertical plane that passes through \(P\) in the direction of \(u\) intersects \(S\) in a curve \(C\). Then, the sople of the tagent line \(T\) to \(C\) at the point \(P\) is the rate of change of \(z\) in the direction of \(u\).
Now, consider another point \(Q(x,y,z)\) on \(C\) and \(P', Q'\) are the projections of \(P, Q\) onto the \(xy\)-plane, then the vector \(\overrightarrow{P'Q'}\) is parallel to \(u\). So,
\(\)\overrightarrow{P’Q’}\(= hu = \left\langle ha, hb \right\rangle\)
for some scalar h. Hence,
\[x - x_0 = ha,\ x = x_0 + ha\] \[y - y_0 = hb,\ y=y_0 + hb\]and
\[\frac{\Delta z}{h} = \frac{z - z_0}{h} = \frac{f(x_0 + ha, y_0 + hb) - f(x_0, y_0)}{h}\]Let’s now take the limit \(h \rightarrow 0\), then we get the rate of change of \(z\) in the direction of \(u\), which is called the directional derivative of \(f\) in the direction of \(u\).
Definition
\[D*u f(x_0, y_0) = \lim*{h \rightarrow 0} = \frac{f(x_0 + ha, y_0 + hb) - f(x_0, y_0)}{h}\]The directional derivative of \(f\) at \((x_0, y_0)\) in the direction of a unit vector \(u = \left\langle a, b \right\rangle\) is
[Note] Notice that if \(u = \left\langle 1, 0 \right\rangle\), then \(D_uf = f_x\). So the partial derivatives of \(f\) with respect to \(x\) or \(y\) are just the special cases of directional derivative.
Directional derivative formula
\[D_uf(x,y) = f_x(x,y)a + f_y(x,y)b\]If \(f\) is a differentiable function of \(x\) and \(y\), then \(f\) has a directional derivative in the direction of any unit vector \(u = \left\langle a, b, \right\rangle\) and
Gradient Vector
From the above equation to find the directional derivative, we can re-write it as the dot product of two vectors
\[D_uf(x,y) = f_x(x,y)a + f_y(x,y)b\] \[= \begin{pmatrix} f_x(x,y) \\\ f_y(x,y)\end{pmatrix} \cdot \begin{pmatrix} a \\\ b \end{pmatrix}\] \[= \begin{pmatrix} f_x(x,y) \\\ f_y(x,y)\end{pmatrix} \cdot u\]The first vector \(\left\langle f_x(x,y), f_y(x,y) \right\rangle\) appears in many other contexts so we give it a special name, the gradient of \(f\) and a special notation \(\nabla f\).
Definition
\[\nabla f(x,y) = \left\langle f_x(x,y), f_y(x,y) \right\rangle = \frac{\partial f}{\partial x}i + \frac{\partial f}{\partial y}j\]If \(f\) is a function of two variables \(x\) and \(y\), then the gradient of \(f\) is the vector function \(\nabla f\) defined by
Hence, we can express the directional derivative using the gradient.
\[D_uf(x,y) = f_x(x,y)a + f_y(x,y)b\] \[= \nabla f(x,y) \cdot u\][Note] Function of more than two variables works the exact same way.
Maximizing the Diectional Derivative
Now comes an important part (used in machine learning all the time): in which of these directions does \(f\) change fastest and what is the maximum rate of change?
Suppose \(f\) is a differentiable function of two more three variables. The maximum value of the directional derivative \(D_uf(x)\) is \(\lvert \nabla f(x) \rvert\) and it occurs when \(u\) has the same direction as the gradient vector \(\nabla f(x)\).
Proof
The proof is quite simple.
\[D_u f = \nabla f \cdot u = \lvert \nabla f \rvert \lvert u \rvert \cos{\theta}\] \[= \lvert \nabla f \rvert \cos{\theta}\]where \(\theta\) is the angle between \(\nabla f\) and \(u\). The maximum value of \(\cos{\theta}\) is 1 when \(\theta = 0\). Hence, the maximum value of \(D_u f\) is \(\lvert \nabla f \lvert\) and it occurs when \(\theta = 0\) which means \(u\) has the same direction as \(\nabla f\).
In summary, we can easily calculate the maximum value of the direction derivative at a given point. This is the foundation of gradient descent algorithm widely used in machine learning and deep learning literature.
Tangent Planes to Level surfaces
Suppose \(S\) is a level surface with equation \(F(x,y,z) = k\) and let \(P(x_0, y_0, z_0)\) be a point on \(S\). Let \(C\) be any curve that lies on the surface \(S\) and passes through the point \(P\). The curve \(C\) is described by a vector function \(r(t) = \left\langle x(t), y(t), z(t) \right\rangle\). Let \(t_0\) be the parameter value corresponding to \(P\) so \(r(t_0) = \left\langle x_0, y_0, z_0) \right\rangle\). Since \(C\) lies on \(S\), any point \((x(t), y(t), z(t))\) must satisfy the equation of \(S\):
\[F(x(t), y(t), z(t)) = k\]If \(x,y,z\) are differentiable functions of \(t\) and \(F\) is also differentiable, we can apply chain rule:
\[\frac{\partial F}{\partial x}\frac{dx}{dt} + \frac{\partial F}{\partial y}\frac{dy}{dt} + \frac{\partial F}{\partial z}\frac{dz}{dt} = 0\]Since \(\nabla F = \left\langle F_x, F_y, F_z \right\rangle\) and \(r'(t) = \left\langle x'(t), y'(t), z'(t) \right\rangle\), we can rewrite using dot product,
\[\nabla F \cdot r'(t) = 0\]In particular, when \(t=t_0\) we have \(r(t_0) = \left\langle x_0, y_0, z_0 \right\rangle\). So,
\[\nabla F(x_0, y_0, z_0) \cdot r'(t_0) = 0\]This says that the gradient vector at P is perpendicular to the tangent vector \(r'(t_0)\) to any curve \(C\) on \(S\) that passes through \(P\). If \(\nabla F(x_0, y_0, z_0) \neq 0\), it is natural to define the tangent plane to the level surface \(F(x,y,z)=k\) at \(P(x_0,y_0,z_0)\) as the plane that passes through \(P\) and has normal vector \(\nabla F(x_0, y_0, z_0)\). Using the equation for a plane, we can write the equation of this tangent plane as
\[F_x(x_0,y_0,z_0)(x-x_0) + F_y(x_0,y_0,z_0)(y-y_0) + F_z(x_0,y_0,z_0)(z-z_0)=0\]The normal line to \(S\) at \(P\) is the line passing through \(P\) and perpendicular to the tangent plane.
References
[1] Stewart Calculus, 8th edition