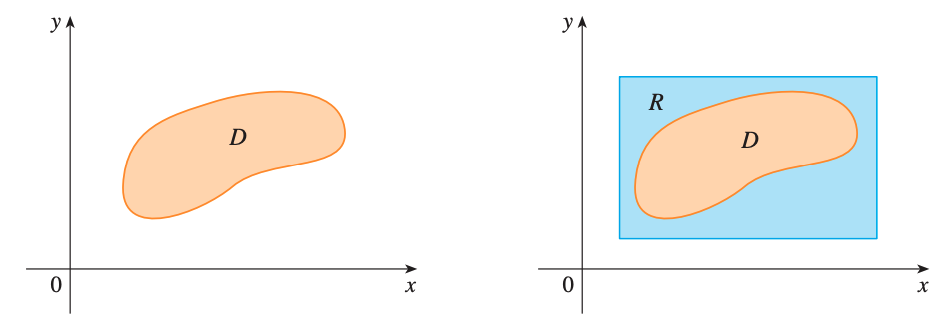
Double Integral of \(f\) over \(D\)
Often we want to evaluate integrals not just over rectangles but also over general region \(D\). We suppose that \(D\) is a bounded region so that it can be enclosed with a rectangle as shown in the figure.
We define a new function \(F\) such that
\[F(x,y) = \begin{cases} f(x,y) & \text{if}\ (x,y)\ \text{is in}\ D \\\ 0 & \text{if}\ (x,y)\ \text{is in}\ R\ \text{but not in}\ D\end{cases}\]Double Integral over \(D\)
If \(F\) is integrable over \(R\), then we define the double integral of \(f\) over \(D\) by
\[\iint_D f(x,y)dA = \iint_R F(x,y)dA\]This makes sense because those regions not in \(D\) but in \(R\) do not contribute to the integral in the first place.
Type I Region
A plane region \(D\) is said to be of type I if it lies between the graphs of two continuous functions of \(x\),
\[D = \{ (x,y)\ \vert \ a \leq x \leq b, g_1(x) \leq y \leq g_2(x) \}\]where \(g_1, g_2\) are continuous on \([a,b]\).
Then,
\[\iint*D f(x,y)dA = \int_a^b\int*{g_1(x)}^{g_2(x)}f(x,y)dydx\]Type II Region
Planes regions of type II are defined as
\[D = \{ (x,y)\ \vert \ c \leq y \leq d, h_1(y) \leq x \leq h_2(y) \}\]where \(h_1, h_2\) are continuous.
Then,
\[\iint*D f(x,y)dA = \int_c^d \int*{h_1(y)}^{h_2(y)}f(x,y)dxdy\]Properties of Double Integrals
We assume that all of the integrals of the following properties exist.
\[[1]\ \iint_D [f(x,y) + g(x,y)]dA = \iint_Df(x,y)dA + \iint_Dg(x,y)dA\] \[[2]\ \iint_D cf(x,y)dA = c \iint_D f(x,y)dA\]if \(f(x,y) \geq g(x,y)\) for all \((x,y)\) in \(D\), then
\[[3]\ \iint_D f(x,y)dA \geq \iint_D g(x,y)dA\]If \(D=D_1 \cup D_2\) where \(D_1\) and \(D_2\) don’t overlap except perhaps boundaries, then
\[[4]\ \iint*D f(x,y)dA = \iint*{D*1}f(x,y)dA + \iint*{D_2}f(x,y)dA\]If we integrate the constant function \(f(x,y)=1\) over a region \(D\), we get the area of \(D\),
\[[5] \iint_D 1 dA = A(D)\]If \(m \leq f(x,y) \leq M\) for all \((x,y)\) in \(D\), then
\[m A(D) \leq \iint_D f(x,y)dA \leq MA(D)\]References
[1] Stewart Calculus, 8th edition