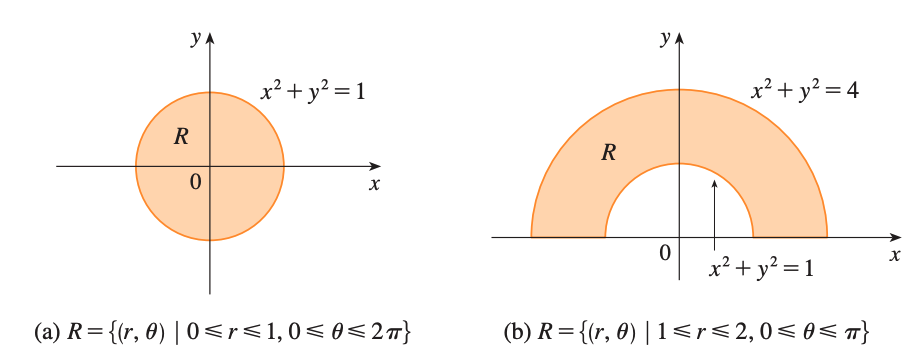Double Integrals in Polar Coordinates
 |
|---|
| stewart-calculus-8th-edition |
Suppose we want to evaluate a double integral \(\iint_Rf(x,y)dA\) but it’s quite complicated to descript using a rectangle. Instead, we can simply use polar coordinates to evaluate the double integral
\[r^2 = x^2 + y^2\ \ \ \ x=r\cos{\theta}\ \ \ \ \ y=r\sin{\theta}\]Then, the regions in the figure above are some cases of polar rectangle
\[R = \{ (r,\theta)\ \vert \ a \leq r \leq b, \alpha \leq \theta \leq \beta \}\]Using this we can evaluate the integrals more easily
Definition
If \(f\) is continuous on a polar rectangle \(AR\) by \(0 \leq a \leq r \leq b\), \(\alpha \leq \theta \leq \beta\) where \(0 \leq \beta - \alpha \leq 2\pi\), then
\[\iint*R f(x,y)dA = \int*{\alpha}^{\beta}\int_a^b f(r \cos{\theta}, r\sin{\theta})\ r\ dr\ d\theta\]More complicated Region
 |
|---|
| stewart-calculus-8th-edition |
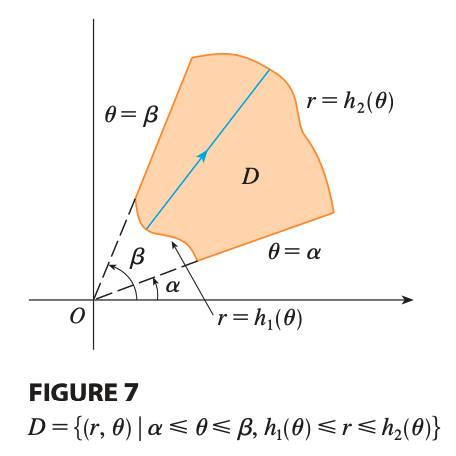
If \(f\) is continuous on a polar region of the form
\[D = \{ (r, \theta)\ \vert \ \alpha \leq \theta \leq \beta, h_1(\theta) \leq r \leq h_2(\theta) \}\]Then,
\[\iint*D f(x,y)dA = \int*{\alpha}^{\beta}\int\_{h_1(\theta)}^{h_2(\theta)}f(r\cos{\theta},r\sin{\theta})\ r\ dr\ d\theta\]References
[1] Stewart Calculus, 8th edition