Surface Area
 |
|---|
| stewart-calculus-8th-edition |
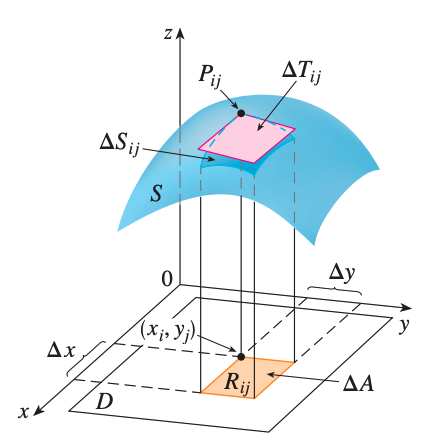
The surface of \(S\) is defined as
\[A(S) = \lim*{m,n \rightarrow \infty} \sum*{i=1}^m \sum*{j=1}^n \Delta T*{ij}\]Surface Area by double integral
 |
|---|
| stewart-calculus-8th-edition |
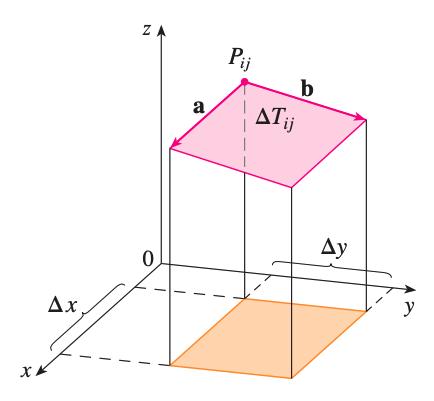
To find a more convenient way of finding surface area, let \(a\) and \(b\) be the vectors starting at \(P_{ij}\) and lie along the sides of the parallelogram with area \(\Delta T_{ij}\). Then,
\[\Delta T\_{ij} = \lvert a \times b \rvert\]But \(f_x(x_i, y_j)\) and \(f_y(x_i, y_j)\) are the slopes of the tangent lies through \(P_{ij}\) in the directions of \(a\) and \(b\). Hence,
\[a = \Delta x \hat{i} + f_x(x_i, y_j) \Delta x \hat{k}\] \[b = \Delta y \hat{j} + f_y(x_i, y_j) \Delta y \hat{k}\]Then,
\[a \times b = \begin{vmatrix} i & j & k \\\ \Delta x & 0 & f_x(x_i, y_j)\Delta x \\\ 0 & \Delta y & f_y(x_i, y_j)\Delta y \end{vmatrix}\] \[= (-f_x(x_i,y_j)\hat{i} - f_y(x_i,y_j)\hat{j}+\hat{k})\Delta A\]Hence,
\[\Delta T\_{ij} = \lvert a \times \rvert = \sqrt{f_x(x,y)^2 + f_y(x,y)^2 + 1} \Delta A\]From the definition in the first section,
\[A(S) = \lim*{m,n \rightarrow \infty}\sum*{i=1}^m \sum\_{j=1}^n \sqrt{f_x(x,y)^2 + f_y(x,y)^2 + 1} \Delta A\]With the definition of a dougle integral, we finally get
Definition
\[A(S) = \iint_D \sqrt{f_x(x,y)^2 + f_y(x,y)^2 + 1} dA\]or
\[A(S) = \iint_D \sqrt{1 + \left( \frac{\partial z}{\partial x} \right)^2 + \left( \frac{\partial z}{\partial y} \right)^2} dA\]References
[1] Stewart Calculus, 8th edition