Triple Integrals
If \(f\) is continuous on the rectangular box \(B = [a,b] \times [c,d] \times [r,s]\), then
\[\iiint_B f(x,y,z)dV = \int_r^s \int_c^d \int_a^b f(x,y,z)dxdydz\] |
|---|
| stewart-calculus-8th-edition |
Now we define the triple integral over a general bounded region E in 3D space.
Type I for E
 |
|---|
| stewart-calculus-8th-edition |
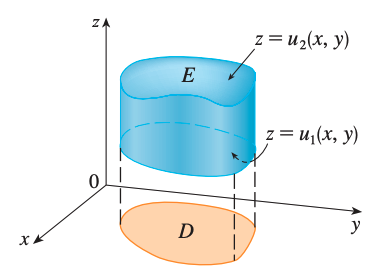
A solid region \(E\) is said to be of type I if it lies between the graphs of two continuous functions of \(x\) and \(y\),
\[E = \{ (x,y,z) \vert (x,y) \in D, u_1(x,y) \leq z \leq u_2(x,y) \}\]where \(D\) is the projection of \(E\) onto the xy-plane. Then the integral is
\[\iiint*E f(x,y,z)dV = \iint_D \left[ \int*{u_1(x,y)}^{u_2(x,y)} f(x,y,z)dz \right]dA\]Type I for D
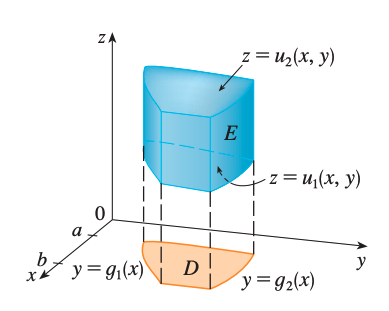
The projection \(D\) of \(E\) onto the xy-plane is a type I plane region, then
\[E = \{ (x,y,z)\ \vert\ a \leq x \leq b, g_1(x) \leq y \leq g_2(x), u_1(x,y) \leq z \leq u_2(x,y) \}\]then,
\[\iiint*E f(x,y,z)dV = \int_a^b \int*{g*1(x)}^{g_2(x)}\int*{u_1(x,y)}^{u_2(x,y)}f(x,y,z)dzdydx\]Type II for D
If \(D\) is a type II plane region, then
\[E = \{ (x,y,z)\ \vert \ c \leq y \leq d, h_1(y) \leq x \leq h_2(y), u_1(x,y) \leq z \leq u_2(x,y) \}\]then,
\[\iiint*E f(x,y,z)dV = \int_c^d \int*{h*1(y)}^{h_2(y)}\int*{u_1(x,y)}^{u_2(x,y)}f(x,y,z)dzdxdy\]References
[1] Stewart Calculus, 8th edition