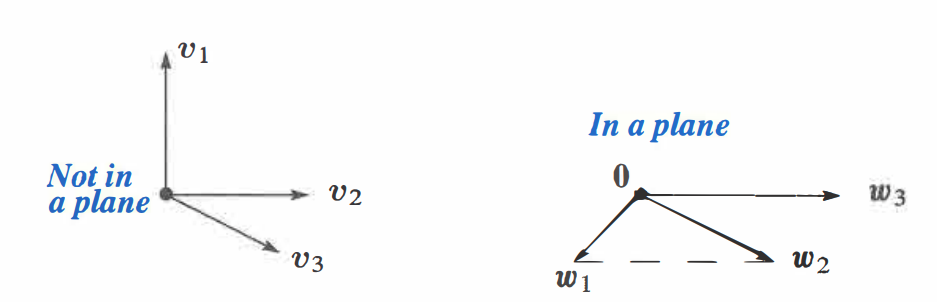Keywords
[1] Independent columns of \(A\): The only solution to \(Ax=0\) is \(x=0\). The nullspace is \(Z\)
[2] Independent vectors: The only zero combination \(c_1v_1 + \cdots + c_kv_k = 0\) has all \(c's=0\)
[3] A matrix with \(m < n\) has dependent columns: At least \(n-m\) free variables / special solutions
[4] The vectors \(v_1,...,v_k\) span the space \(S\) if \(S\)=all combinations of the \(v\)’s
[5] The vectors \(v_1,...,v_k\) are a basis for \(S\) if they’re independent and they span \(S\)
[6] The dimension of a space \(S\) is the number of vectors in every basis for \(S\)
[7] If \(A\) is 4 by 4 and invertible, its columns are a basis for \(\mathbb{R}^4\). The dimension of \(\mathbb{R}^4\) is 4.
Overview
What is the true dimension of a subspace? Take an m x n matrix as an example. What is the true dimension of the column space? It’s not just \(n\). The dimension is measured by the number of independent columns which is teh rank \(r\).
The idea of independence applies to any vectors \(v_1,...,v_n\) in any vector space. The “vectors” might not be column vectors but also can be matrices or functions. But we mostly focus on the column space and nullspace of \(A\) in this chapter.
Our goal is to understand a basis which is independent vectors that “span” the space.
Every vector in the space is a unique combination of the basis vectors
4 Essential Ideas
Linear Independence
Definition
The columns of \(A\) are linearly independent when the only solution to \(Ax=0\) is \(x=0\).
or more generally for any sequence of vectors \(v_1,...,v_n\),
The sequence of vectors \(v_1,...,v_n\) is linearly independent if \(x_1v_1+x_2v_2+ \cdots + x_nv_n=0\) only happens when all \(x\)’s are \(0\)
In other words, the columns are independent when nullspace of A, \(N(A)\), contains only the zero vector.
We can intuitively understand the independence with an example of three vectors in \(\mathbb{R}^3\).
[Independent] If three vectors \(v_1, v_2, v_3\) are not in the same plane, they are independent.
[Dependent] if three vectors \(v_1, v_2, v_3\) are in the same plane, they are dependent.
For the left example, the only case when the linear combination of those vectors is \(0\) is \(0v_1 + 0v_2 + 0v_3\), thus independent. However, for the right example, \(w_1-w_2+w_3\) gives the zero vector, thus dependent.
Examples
Let’s look at some examples for independent and dependent vectors.
(i) \((1,0)\) and \((0,1)\) are independent
(ii) \((1,1)\) and \((-1,-1)\) are dependent
(iii) \((1,1)\) and \((0,0)\) are dependent because of the zero vector
(iv) In \(\mathbb{R^2}\), any three vectors are dependent.
The first three are obvious. But why is the fourth case? Three vectors in \(\mathbb{R}^2\) cannot be independent because \(A\) must have a free variable so there’s a special solution to \(Ax=0\). Another interpretation is that the combination of two vectors will produce the third vector.
More generally,
Any set of \(n\) vectors in \(\mathbb{R}^m\) must be linearly dependent if \(n > m\).
Full Column rank
The columns of \(A\) are independent exactly when the rank is \(r=n\). There are \(n\) pivots and no free variables. Only \(x=0\) is in th e nullspace.
Span
The most popular subspace is the column space which is filled with all combinations of the columns. We can simplify this using the single word span: The column space is spanned by the columns
Definition
A set of vectors spans a space if their linear combinations fill the space.
So the columns of a matrix span its column space. But notice that they might be dependent.
Row Space
We mainly talked about the column space. It’s time to look at the row space.
The row space of a matrix is the subspace of \(\mathbb{R}^n\) spanned by the rows. Also, the row space of \(A\) is \(C(A^T)\). It is the column space of \(A^T\).
Basis
Two vectors cannot span all of \(\mathbb{R}^3\) even if they’re independent. Four vectors cannot be independent even if they span \(\mathbb{Rd^3}\). We want “just enough” independent vectors to span the space. This is a basis.
Definition
A basis for a vector space is a sequence of vectors that are linearly independent and they span the space.
Every vector \(v\) in the space is a combination of the basis vectors since they span the space. More importantly, the combination that produces \(v\) is unique because the basis vectors \(v_1,...,v_n\) are not two ways to produce \(v\).
Standard Basis
For example, the columns of \(I = \begin{bmatrix} 1 & 0 \\\ 0 & 1 \end{bmatrix}\) produce the standard basis for \(\mathbb{R}^2\). The basis vectors are \(i = \begin{bmatrix} 1 \\\ 0 \end{bmatrix}\) and \(j = \begin{bmatrix} 0 \\\ 1 \end{bmatrix}\) and they’re independent. They span \(\mathbb{R}^2\)
Or the columns of the n x n identity matrix give the standard basis for \(\mathbb{R}^n\).
Column space and Basis
One important property of an invertible matrix is
The columns of every invertible n by n matrix give a basis for \(\mathbb{R}^n\)
One observation we can make is
The vectors \(v_1,...,v_n\) are a basis for \(\mathbb{R}^n\) exactly when they’re the columns of an \(n\) by \(n\) invertible matrix. Therefore, \(\mathbb{R}^n\) has infinitely many different bases.
There’s only one way to produce a vector \(v\) with a basis but there’re infinite ways of producing a vector space! Don’t get confused.
A more general version of this rule is by observing the pivots.
The pivot columns of \(A\) are a basis for its column space. The pivot rows of \(A\) are a basis for its row space (so are the pivot rows of its echelon form \(R\))
Dimension of a Space
Here comes another extremely important rule:
The dimension of a space is the number of vectors in every basis. If \(v_1,...,v_m\) and \(w_1,...,w_n\) are both bases for the same vector space, then \(m=n\)
The dimension counts the “degrees of freedom” in the space. The dimension of \(\mathbb{R}^n\) is \(n\). Also, the dimension of the columns space is equal to the rank of the matrix.
References
[1] Introduction to Linear Algebra, 5th edition