Keywords
[1] The column space \(C(A)\) and the row space \(C(A^T)\) both have dimension \(r\) (the rank of \(A\))
[2] The nullspace \(N(A)\) has dimension \(n-r\). The left nullspace \(N(A^T)\) has dimension \(m-r\)
[3] Elimination produces bases for the row space and nullspace of \(A\): They’re the same for \(\mathbb{R}\)
[4] Elimination often changes the column space and left nullspace (but dimensions don’t change)
[5] Rank one matrices: \(A=uv^T=\text{column times row}\): \(C(A)\) has basis \(u\), \(C(A^T)\) has basis \(v\).
Four Fundamental Subspaces
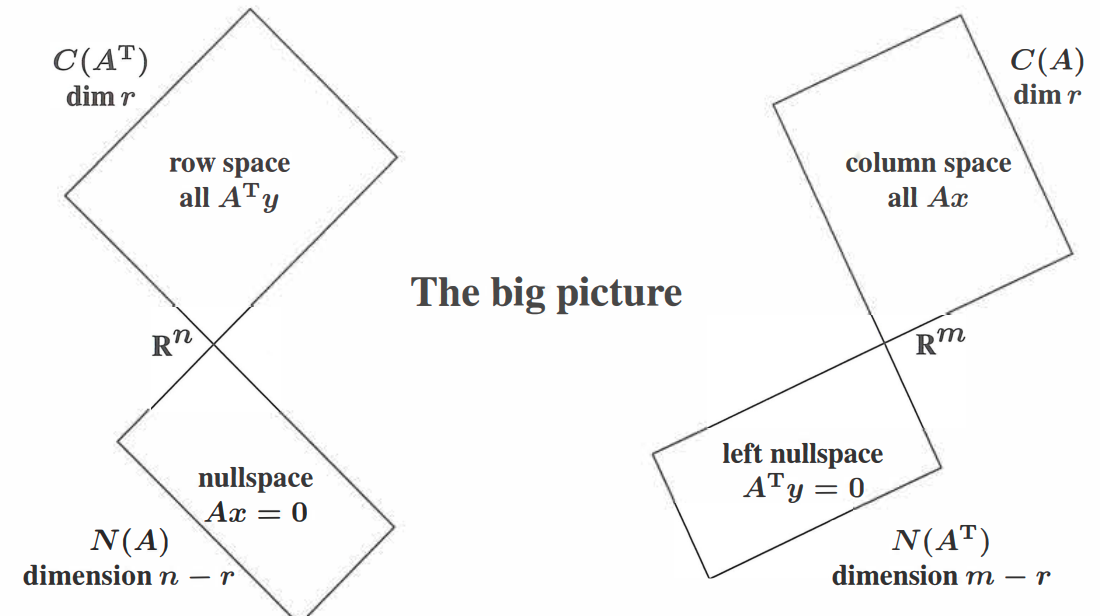
The rank of a matrix is the number of pivots. The dimension of a subspace is the number of vectors in a basis. So we count pivots or basis vectors. The rank of \(A\) reveals the dimensions of ALL four fundamental subspaces. Let’s first what those four fundamental subspaces are
[1] The row space is \(C(A^T)\), a subspace of \(\mathbb{R}^n\)
[2] The column space is \(C(A)\), a subspace of \(\mathbb{R}^m\)
[3] The nullspace is \(N(A)\), a subspace of \(\mathbb{R}^n\)
[4] The left nullspace is \(N(A^T)\), a subspace of \(\mathbb{R}^m\). This is our new space.
The row space of \(A\) is the column space of \(A^T\). The left nullspace solves \(A^Ty=0\) which is the nullspace of \(A^T\). The vectors \(y\) go on the left side of \(A\).
Part 1 Fundamental Theorem - Dimensions of four subspaces
We’ll look at the dimensions of the four fundamental subspaces.
The row space and column space have the same dimension \(r\) which is the rank of the matrix.
\(N(A)\) and \(N(A^T)\) have dimensions \(n-r\) and \(m-r\), to make up the full \(n\) and \(m\).
The Four Subspaces for \(A\)
The subspace dimensions for \(A\) are the same as for \(\mathbb{R}\). \(A\) is any matrix that reduces down to \(R = rref(A)\).
Row space \(C(A^T)\)
\(A\) has the same row space as \(R\). Same dimension \(r\) and same basis.
The reason is that the rows of \(A\) are a combination of the rows of \(R\) and vice-versa. Elimination changes rows, but now row spaces.
Column space \(C(A)\)
The column space of \(A\) has dimension \(r\). The column rank equals the row rank.
[NOTE] Rank Theorem: The number of independent columns = number of independent rows
Be careful that \(A\) and \(R\) might have different spaces. The right reason is that the same combinations of the columns are zero (or nonzero) for \(A\) and \(R\). In other words, \(Ax=0\) exactly when \(Rx=0\). The column spaces are different but their dimensions are the same - equal to \(r\).
So the \(r\) pivots columns of \(A\) are a basis for its column space \(C(A)\).
Nullspace \(N(A)\)
\(A\) has the same nullspace as \(R\). Same dimension \(n-r\) and same basis
This is because the eliminiation does not change the solution space. The special solutions are a basis for the nullspace. There’re \(n-r\) free variables, so the dimension of \(N(A)\) is \(n-r\). So the dimension of column space + dimension of nullspace gives us the dimension of the whole subspace. This is the counting theorem: \(r + (n-r) = n\).
\[dim(C(A)) + dim(N(A)) = dim(\mathbb{R}^n)\]Left Nullspace \(N(A^T)\)
The left nullspace of \(A\) (nullspace of \(A^T\)) has dimension \(m-r\)
If we know \(A\), then we know \(A^T\). Since \(A^T\) is \(n\) by \(m\), the whole space is now \(\mathbb{R}^m\). The counting rule for this new \(A^T\) is \(r + (m-r) = m\). The left nullspace solve \(A^Ty=0\). In other words, \(y^TA=0\) so the \(y\)’s in the left nullspace combine the rows to give the zero row.
References
[1] Introduction to Linear Algebra, 5th edition