Keywords
[1] Orthogonal vectors have \(v^Tw=0\). Then \(\lVert v \rVert^2 + \lVert w \rVert^2 = \lVert v + w \rVert^2 = \lVert v - w \rVert^2\)
[2] Subspaces \(V\) and \(W\) are orthogonal when \(v^Tw=0\)for every \(v\) in \(V\) and every \(w\) in \(W\).
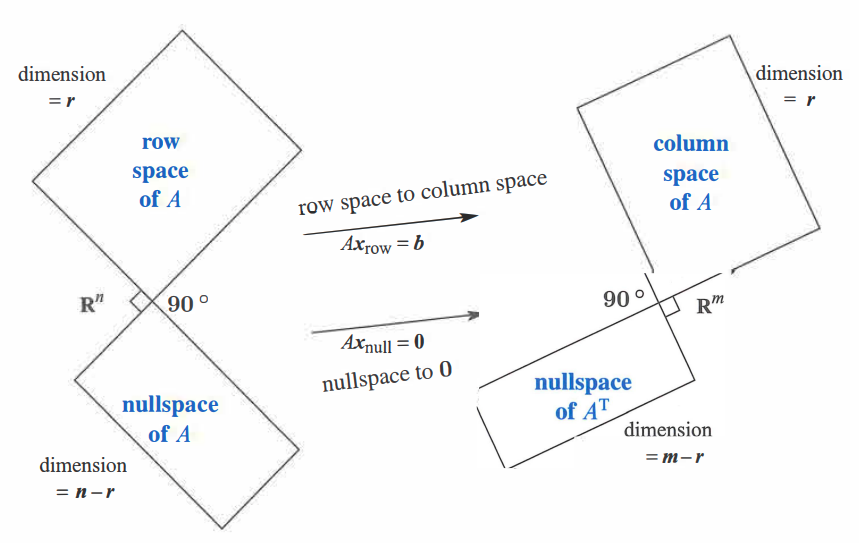
[3] The row space of \(A\) is orthogonal to the nullspace. The column space is orthogonal to \(N(A^T)\)
[4] One pair of dimensions adds to \(r + (n-r)=n\). The other pair has \(r+(m-r)=m\).
[5] Row space and nullspace are orthogonal complements: Every \(x\) in \(\mathbb{R}^n\) splits into \(x_{row}+x_{null}\)
[6] Suppose a space \(S\) has dimension \(d\). Then every basis for \(S\) consists of \(d\) vectors
[7] If \(d\) vectors in \(S\) are independent, they span \(S\). If \(d\) vectors span \(S\), they are independent.
Orthogonal vectors
Two vectors are orthogonal when their dot product is zero: \(v \cdot w = v^Tw = 0\). Why is that? Remember the Pythagorean Theorem: \(a^2+b^2=c^2\) for a right triangle.
Orthogonal vectors imply \(\lVert v \rVert^2 + \lVert w \rVert^2 = \lVert v + w \rVert^2\). We can re-write it as
\[v^Tv + w^Tw = (v+w)^T(v+w)\] \[v^Tv + w^Tw = (v^T+w^T)(v+w)\] \[v^Tv + w^Tw = v^Tv+w^Tw+v^Tw+vw^T\]For this equation to be satisfied, we must have \(v^Tw=w^Tv=0\)
Orthogonal subspaces
Two subspaces \(V\) and \(W\) of a vector space are orthogonal if every vector \(v\) in \(V\) is perpendicular to every vector \(w\) in \(W\):
\(v^Tw=0\) for all \(v\) in \(V\) and all \(w\) in \(W\).
When a vector is in two orthogonal subspaces, it must be zero. It is perpendicular to itself as \(0 \cdot 0 = 0\). For example, zero is the only point where the nullspace meets the row space.
Row space is orthogonal to Nullspace
Every row of \(A\) is perpendicular to every vector \(x\) in the nullspace of \(Ax=0\). This is obvious because \(Ax=0\) (think matrix multiplication).
The nullspace \(N(A)\) and the row space \(C(A^T)\) are orthogonal subspaces of \(\mathbb{R}^n\).
Column space is orthogonal to Left Nullspace
When \(b\) is outside the column space, we can’t solve \(Ax=b\). The reason is the same. The nullspace of \(A^T\) is orthogonal to the row space of \(A^T\) which is equal to the column space of \(A\). Hence, every vector \(y\) in the nullspace of \(A^T\) is perpendicular to every column of \(A\).
The left nullspace \(N(A^T)\) and the column space \(C(A)\) are orthogonal in \(\mathbb{R}^m\)
Orthogonal Complements
The orthogonal complement of a subspace \(v\) contains every vector that is perpendicular to \(V\). This orthogonal subspace is denoted by \(V^{\perp}\).
By this definition, the nullspace is the orthogonal complement of the row space. Every \(x\) that is perpendicular to the rows satisfies \(Ax=0\) and lies in the nullspace.
The reverse is also true. If \(v\) is orthogonal to the nullspace, it must be in the row space.
Fundamental Theorem of Linear Algebra, Part 2
\(N(A)\) is the orthogonal complement of the row space \(C(A^T)\) (in \(\mathbb{R}^n\))
\(N(A^T)\) is the orthogonal complement of the column space \(C(A)\) (in \(\mathbb{R}^m\))
The “complement” suggests that every \(x\) can be split into a row space component \(x_r\) and a nullspace component \(x_n\). When \(A\) multiplies \(x=x_r + x_n\).
The nullspace component goes to zero: \(Ax_n = 0\)
The row space component goes to the column space: \(Ax_r=Ax\)
So every vector goes to the column space. Every vector \(b\) in the column space comes from one and only one vector \(x_r\) in the row space
References
[1] Introduction to Linear Algebra, 5th edition