Keywords
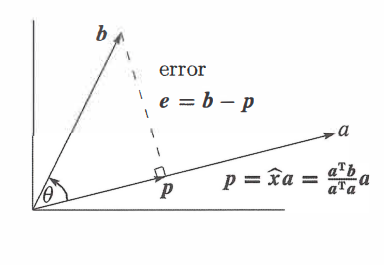
[1] The projection of a vector \(b\) onto the line through \(a\) is the closest point \(p = a\frac{a^Tb}{a^Ta}\)
[2] The error \(e = b - p\) is perpendicular to \(a\): Right triangle \(bpe\) has \(\lVert p \rVert^2 + \lVert e \rVert^2 = \lVert b \rVert^2\)
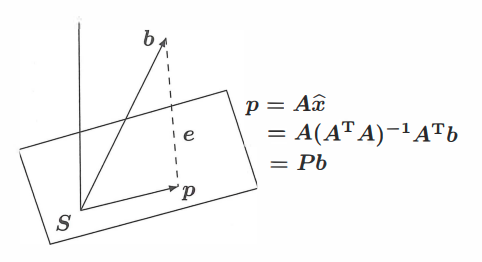
[3] The projection of \(b\) onto a subspace \(S\) is the cloest vector \(p\) in \(S\); \(b-p\) is orthogonal to \(S\).
[4] \(A^TA\) is invertible (and symmetric) only if \(A\) has independent columns: \(N(A^TA)=N(A)\)
[5] Then the projection of \(b\) onto the column space \(A\) is the vector \(p = A(A^TA)^{-1}A^Tb\)
[6] The projection matrix onto \(C(A)\) is \(p=A(A^TA)^{-1}A^T\). It has \(p=Pb\) and \(P^2=P=P^T\)
Project onto a Line
 |
|---|
| Introduction to Linear Algebra, 5th edition |
Suppose a line \(a\) going through the origin. Along that line, we want to find the point \(p\) closest to \(b\). The key to projection is orthogonality
The line from \(b\) to \(p\) is perpendicular to the vector \(a\).
Then, the projection \(p\) will be some multiple of \(a\) so we call \(p=\hat{x}a\).
Now we use a bit of algebra.
\[e = b - p\] \[p=\hat{x}a\] \[e = b - \hat{x}a\] \[a^T(b-\hat{x}a)=0,\ \text{since a is perpendicular to e}\] \[\hat{x}a^Ta = a^Tb\] \[\therefore \hat{x} = \frac{a^Tb}{a^Ta}\] \[\therefore p = \frac{a^Tb}{a^Ta}a\]The projection of \(b\) onto the line through \(a\) is the vector \(p = \hat{x}a = \frac{a^Tb}{a^Ta}a\)
Special cases
[1] If \(b=a\) then \(\hat{x}=1\). Then, the projection of \(a\) onto \(a\) is itself: \(Pa=a\)
[2] If \(b\) is perpendicular to \(a\), then \(a^Tb=0\) so the projection is \(p=0\)
Projection Matrix \(P\)
In the formula of \(p\), what matrix is multiplying \(b\)? We can decompose it into
\[p = \frac{a^Tb}{a^Ta}a = \left( \frac{aa^T}{a^Ta} \right) b = Pb\]The projection matrix \(P=\frac{aa^T}{a^Ta}\)
The rank of \(P\) is \(1\) and \(p\) is in \(C(P)\).
Projection onto a Subspace
 |
|---|
| Introduction to Linear Algebra, 5th edition |
Suppose \(n\) vectors \(a_1,...,a_n\) in \(\mathbb{R}^m\) and these \(a\)’s are linearly independent. Now, we want to find the combination \(p = \hat{x_1}a_1 + \cdots + \hat{x_n}a_n\) closest to a given vector \(b\).
We suppose the matrix \(A\) has columns as \(a_1,...,a_n\). The combinations in \(\mathbb{R}^m\) are the vectors \(Ax\) in the column space. We’re looking for the particular combination \(p = A\hat{x}\), the projection, that is closest to \(b\).
Then,
\[p = A\hat{x}\] \[e = b - p\] \[e = b - A\hat{x}\]But \(e\) is perpendicular to \(A\),
\[A^T(b-A\hat{x})=0\] \[A^Tb = A^TA\hat{x}\]Hence, we get
\[\therefore \hat{x} = (A^TA)^{-1}A^Tb\] \[\therefore p = A\hat{x} = A(A^TA)^{-1}A^Tb\] \[\therefore P = A(A^TA)^{-1}A^T\]where \(p\) is the projection of \(b\) onto \(A\) and \(P\) is the projection matrix.
Notice that since \(e\) is orthogonal to \(C(A)\), \(e\) is in the left-nullspace \(N(A^T)\). Also, \(A^TA\) is invertible only if \(A\) has linearly independent columns.
The projection matrix satisfies \(P^T=P\),\(P^2=P\), and \(Pb=p\)
References
[1] Introduction to Linear Algebra, 5th edition