Jacobian Matrix
Sometimes we need to find all the partial derivatives of a function whose input and output are vectors. A Jacobian matrix contains all such partial derivatives.
For a function \(f : \mathbb{R}^m \rightarrow \mathbb{R}^n\), the Jacobian matrix \(J \in \mathbb{R}^{n \times m}\) is \(J_{i,j} = \frac{\partial}{\partial x_j}f(x)_i\)
For \(f(x1,x2, ..., x_n) = (f_1, f_2, ..., f_m)\), the Jacobian matrix \(J\) is,
\[\begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \dots & \frac{\partial f_1}{\partial x_m}\\\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \dots & \frac{\partial f_2}{\partial x_m} \\\ \vdots & \vdots & \ddots & \vdots \\\ \frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \dots & \frac{\partial f_n}{\partial x_m} \end{bmatrix}\]Second derivative and Curvature
Sometimes we’re also interested in a second derivative. For a function \(f: \mathbb{R}^n \rightarrow \mathbb{R}\), the second derivative with respect to \(x_i\) of the derivative of \(f\) with respect to \(x_j\) is \(\frac{\partial^2}{\partial x_i \partial x_j}f\).
The seceond derivative tells us how the first derivative will change as the input changes. Thus, it also tells us how much a gradient step will impact.
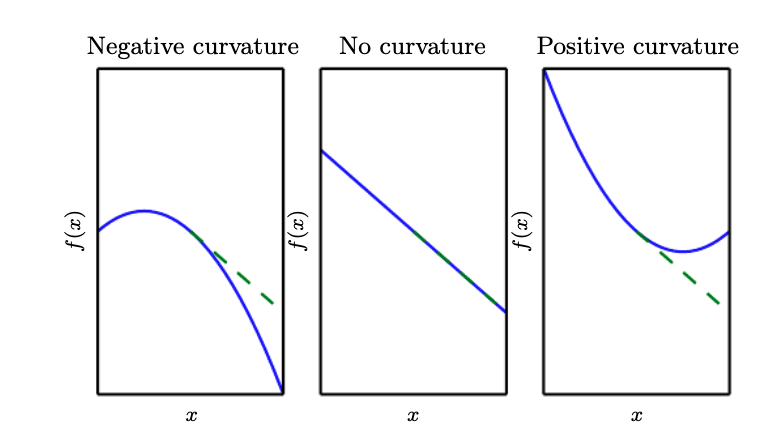
The second derivative can be interpreted as curvature.
If the second derivative is 0, then there’s no curvature. For a perfectly flat line, if we take a step size of \(\epsilon\) along the negative gradient, and the cost function will also equally decrease by \(\epsilon\).
If the second derivative is negative, then \(f\) curves downward, so the cost function will change more than \(\epsilon\).
if the second derivative is positive, then \(f\) curves upward, so the cost function will change less than \(\epsilon\)
Hessian Matrix
The Hessian matrix is a matrix that collects all those second derivatives.
The Hessian matrix \(H(f)(x)\) is defiend such that,
\[H(f)(x)\_{i,j} = \frac{\partial^2}{\partial x_i \partial x_j}f(x)\]Note that the Hessian is the Jacobian of the gradient.
Anywhere that the second partial derivatives are continuous, the differential operators are commutative. So their order can be swapped:
\[\frac{\partial^2}{\partial x_i \partial x_j}f(x) = \frac{\partial^2}{\partial x_j \partial x_i}f(x)\]implying that \(H_{i,j} = H_{j,i}\) so the Hessian matrix is symmetirc at such points. Most functions in the deep learning literature have a symmetric Hessian matrix.