Keywords
[1] 2 by 2: \(ad-bc\) has \(2!\) terms with \(\pm\) signs. n by n: \(det(A)\) adds n! terms with \(\pm\) signs.
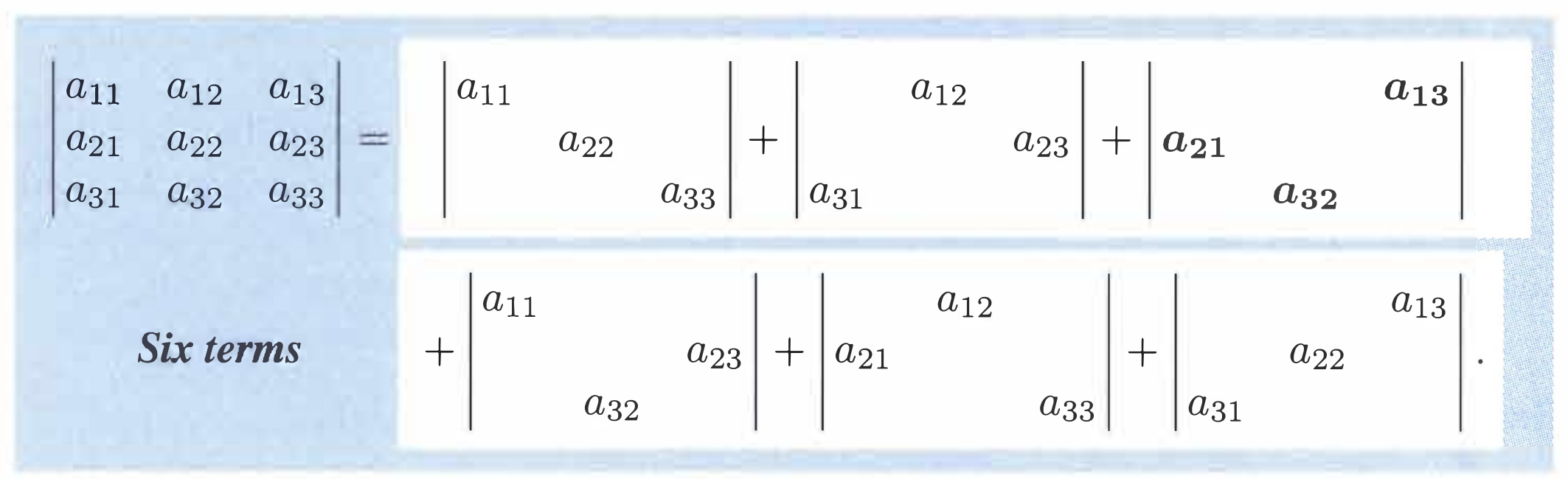
[2] For \(n=3\), \(det(A)\) adds \(3!=6\) terms. Two terms are \(+a_{12}a_{23}a_{31}\) and \(-a_{13}a_{22}a_{31}\). Rows 1, 2, 3, and columns 1, 2, 3 appear once in each term.
[3] That minus sign came because the column order \(3, 2, 1\) needs one exchange to recover \(1, 2, 3\).
[4] The six terms include \(+a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}=a_{11}(a_{22}a_{33}-a_{23}a_{32}) = a_{11}\)(cofactor \(C_{11}\))
[5] Always \(det(A) = a_{11}C_{11}+a_{12}C_{12d+ \cdots + a_{1n}C_{1n}}\). Cofactors are determinants of size \(n-1\).
Three ways to find determinant
We can find the determinent in three ways
- Pivot formula
- Big formula
- Cofactors
Pivot Formula
Elimination leads \(A\) to \(PA=LU\), then the pivots \(d_1,...,d_n\) are on the diagonal of the upper triangular \(U\). Then, the product of the pivots (with sign) is the determinant.
We can show that it’s true very simply.
\[det(P)det(A) = det(L) det(U) = (1)(d_1d_2\cdots d_n)\]Since \(det(P)=\pm 1\),
\[det(A) = \pm d_1d_2 \cdots d_n\]Now, consider the corner submatrix \(A_k\) (first \(k\) pivots). We can find the \(k^{th}\) pivot using the determinant
\[k^{th}\ \text{pivot} = d*k = \frac{det(A_k)}{det(A*{k-1})}\]The Big Formula
The big formula has n! terms. Each product has one entry from each row and each column which is why there’re \(n!\) cases (permutations).
Notice that the sign of the product is determined by the permutation matrix for each product.
For example,
\[\begin{vmatrix} a*{11} & & \\\ & a*{22} & \\\ & & a*{33} \end{vmatrix} = a*{11}a*{22}a*{33}\begin{vmatrix} 1 & & \\\ & 1 & \\\ & & 1 \end{vmatrix}\]Summary
\(det(A)\) = sum over all \(n!\) column permutations \(P=(\alpha, \beta,...,w)\)
\[det(A) = \sum det(P) a*{1\alpha}a*{2\beta}\cdots a\_{nw}\]Cofactor
The determinant can also be found using cofactor. From the big formula above, 3 by 3 matrix has a determinant which is a sum of \(3!\) products. Notice that you can convert the 6 products into 3 pairs.
\[det(A) = a*{11}(a*{22}a*{33}) + a*{12}(a*{23}a*{31}-a*{21}a*{33})+a*{13}(a*{21}a*{32}-a*{22}a\_{31})\]The quantities in parentheses are called cofactors which are 2 by 2 determinants from rows 2 and 3. The first row contributes the factors \(a_{11}, a_{12}, a_{13}\) and the lower rows form the cofactors \(C_{11}, C_{12}, C_{13}\)
Define \(M_{1j}\) is a submatrix with row 1 and column \(j\) removed. Then, the cofactors along row \(1\) are defined,
\[C*{1j} = (-1)^{1+j} det(M*{1j})\]Then, the determinant can be expressed as
\[det(A) = a*{11}C*{11} + a*{12}C*{12} + \cdots + a*{1n}C*{1n}\]General form
The determinant is the dot product of any row \(i\) of \(A\) with its cofactors using other rows:
\[det(A) = a*{i1}C*{i1} + a*{i2}C*{i2} + \cdots + a*{in}C*{in}\]Each cofactor \(C_{ij}\) (order \(n-1\) without row \(i\) and column \(j\)) includes its correct sign:
\[C*{ij} = (-1)^{i+j}det(M*{ij})\]References
[1] Introduction to Linear Algebra, 5th edition