Keywords
[1] \(A^{-1} = \frac{C^T}{det(A)}\). Then, \((A^{-1})\_{ij}=\) cofactor \(C\_{ji}\) divided by the determinant of \(A\)
[2] Cramer’s Rule computes \(x=A^{-1}b\) from \(x_j=det(A\ \text{with column}\ j\ \text{changed to}\ b)\ /\ det(A)\)
[3] Area of parallelogram = \(\vert ad-bc \vert\) if the four corners are \((0,0), (a,b), (c,d), (a+c, b+d)\)
[4] Volume of box = \(\vert det(A) \vert\) if the rows of \(A\) (or columns of \(A\)) give the sides of the boc
[5] The cross product \(w = u \times v\) is \(\begin{vmatrix} i & j & k \\\ u_1 & u_2 & u_3 \\\ v_1 & v_2 & v_3\end{vmatrix}\). Also, \(v \times u = -(u \times v)\). \(w_1, w_2, w_3\) are cofactors of row 1. Notice \(w^Tu=0\) and \(w^Tv=0\).
Cramer’s Rule
Cramer’s Rule solves \(Ax=b\) algebraically not by elimination. The idea is simple and makes sense.
Suppose we have a matrix \(A\). First, we construct an identity matrix \(I\) with its first column replaced by \(x\) then its determinant is \(x_1\). Then, we multiply this matrix with \(A\) and the result becomes \(B_1\).
\[\begin{bmatrix} & & \\\ & A & \\\ & & \end{bmatrix} \begin{bmatrix} x*1 & 0 & 0 \\\ x_2 & 1 & 0 \\\ x_3 & 0 & 1\end{bmatrix} = \begin{bmatrix} b_1 & a*{12} & a*{13} \\\ b_2 & a*{22} & a*{23} \\\ b_3 & a*{32} & a\_{33}\end{bmatrix} = B_1\] \[det(A)(x_1) = det(B_1)\] \[x_1 = \frac{det(B_1)}{det(A)}\]Now we repeat this process for all the other \(x_i\) to get the all solutions.
Cramer’s Rule
If \(det(A)\) is nonzero, then \(Ax=b\) is solved by determinants:
\[x_1 = \frac{det(B_1)}{det(A)}\ \ \ \ x_2 = \frac{det(B_2)}{det(A)}\ \ \ \ \cdots\ \ x_n = \frac{det(B_n)}{det(A)}\]where the matrix \(B_{j}\) is the matrix \(A\) with \(j^{th}\) column replaced by the vector \(b\).
[Note] But Cramer’s Rule evalutes \(n+1\) determinants and each one is the sum of \(n!\) terms, resulting in \((n+1)!\) terms in total. It would be very inefficient to calculate this (factorial increase very quickly).
Explicit Formula for \(x\) using Cramer’s Rule
Let’s take an example of 2 by 2 matrix \(A\). We now find the columns of \(A^{-1}=[x\ y]\) by solving
\[AA^{-1}=I\]We can break down this equation for each \(x\) and \(y\).
\[\begin{bmatrix} a & b \\\ c & d \end{bmatrix} \begin{bmatrix} x_1 \\\ x_2 \end{bmatrix} = \begin{bmatrix} 1 \\\ 0 \end{bmatrix}\] \[\begin{bmatrix} a & b \\\ c & d \end{bmatrix} \begin{bmatrix} y_1 \\\ y_2 \end{bmatrix} = \begin{bmatrix} 0 \\\ 1 \end{bmatrix}\]Now, we need to calculate \(\vert A \vert\) and determinants for \(x_1, x_2, x_3, x_4\).
\[\begin{vmatrix} a & b \\\ c & d \end{vmatrix}\ \ \begin{vmatrix} \textbf{1} & b \\\ \textbf{0} & d\end{vmatrix}\ \ \begin{vmatrix} a & \textbf{1} \\\ c & \textbf{0} \end{vmatrix}\ \ \begin{vmatrix} \textbf{0} & b \\\ \textbf{1} & d\end{vmatrix}\ \ \begin{vmatrix} a & \textbf{0} \\\ c & \textbf{1} \end{vmatrix}\]The last four determinants are \(d, -c, -b, a\). Notice that they’re cofactors!.
Using the Cramer’s Rule, we get
\[x_1 = \frac{d}{\vert A \vert},\ x_2=\frac{-c}{\vert A \vert},\ y_1=\frac{-b}{\vert A \vert},\ y_2=\frac{a}{\vert A \vert}\]Then,
\[A^{-1} = \frac{1}{\vert A \vert}\begin{vmatrix} d & -b \\\ -c & a \end{vmatrix}\]The idea is that \(A^{-1}\) involves the cofactors. The determinant of each \(B_j\) in Cramer’s Rule is a cofactor of \(A\).
Formula
The \(i,j\) entry of \(A^{-1}\) is the cofactor \(C_{ji}\) divided by \(det(A)\):
\[(A^{-1})_{ij} = \frac{C_{ji}}{det(A)}\]or
\[A\_{-1} = \frac{C^T}{det(A)}\]where \(C\) is the cofactor matrix where the cofactors \(C_{ij}\) go into \(C\). The transpose of \(C\) leads to \(A^{-1}\)
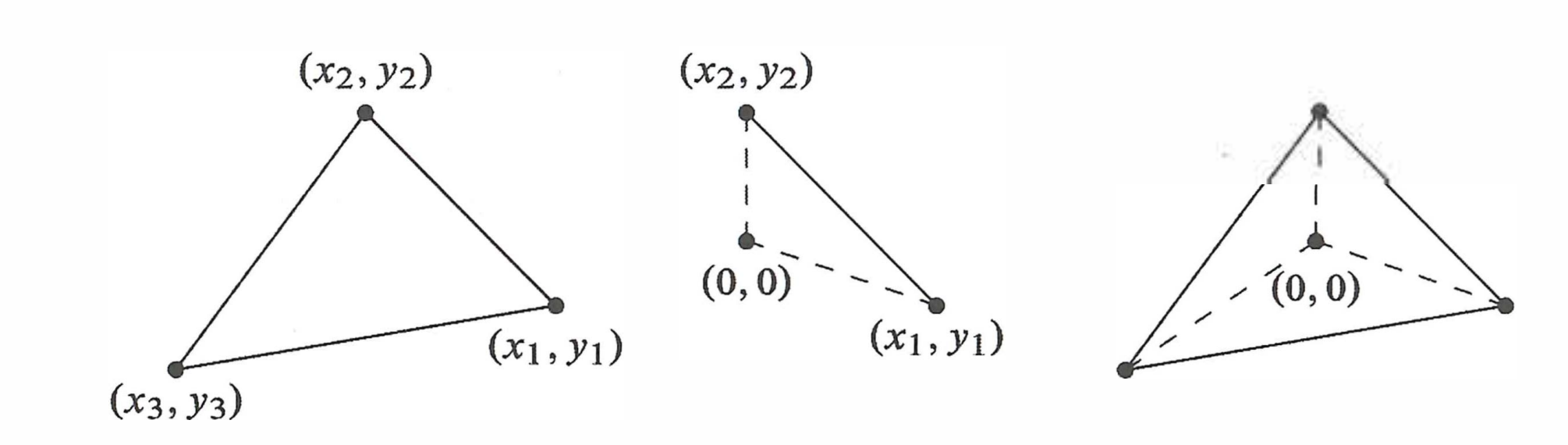
Area of a Triangle
 |
|---|
| Introduction to Linear Algebra, 5th edition |
How do we find the area of a triangle with the corners \((x_1,y_1), (x_2, y_2), (x_3, y_3)\). The best way is to use the determinants.
Area by Determinant
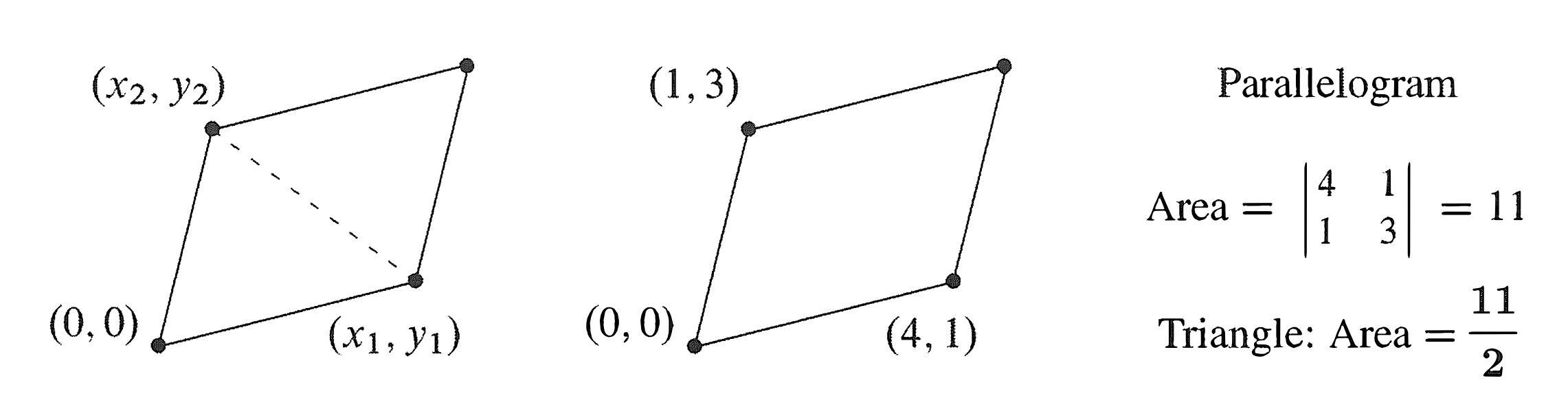
The triangle with corners \((x_1, y_1), (x_2, y_2), (x_3, y_3)\) has \(A = \frac{determinant}{2}\).
\[A = \frac{1}{2} \begin{vmatrix} x_1 & y_1 & 1 \\\ x_2 & y_2 & 1 \\\ x_3 & y_3 & 1\end{vmatrix}\] \[A = \frac{1}{2} \begin{vmatrix} x_1 & y_1 \\\ x_2 & y_2 \end{vmatrix},\ \text{if}\ (x_3,y_3)=(0,0)\]Proof
For the second case, why is the area equal to \(\frac{1}{2} \vert x_1y_2 - x_2y_1 \vert\)?
Consider the case when \((x_3,y_3)=(0,0)\). Let’s remove the factor \(\frac{1}{2}\) to get the parallelogram which is made of two identical triangles.
 |
|---|
| Introduction to Linear Algebra, 5th edition |
This book uses an exotic proof that the area has the same properties as the determinant.
[1] When \(A=I\), the parallelogram becomes the unit square. Its area is \(det(I)=I\)
[2] When rows are exchanged, the determinant reverses sign. The absolute value stays the same - it is the same parallelogram
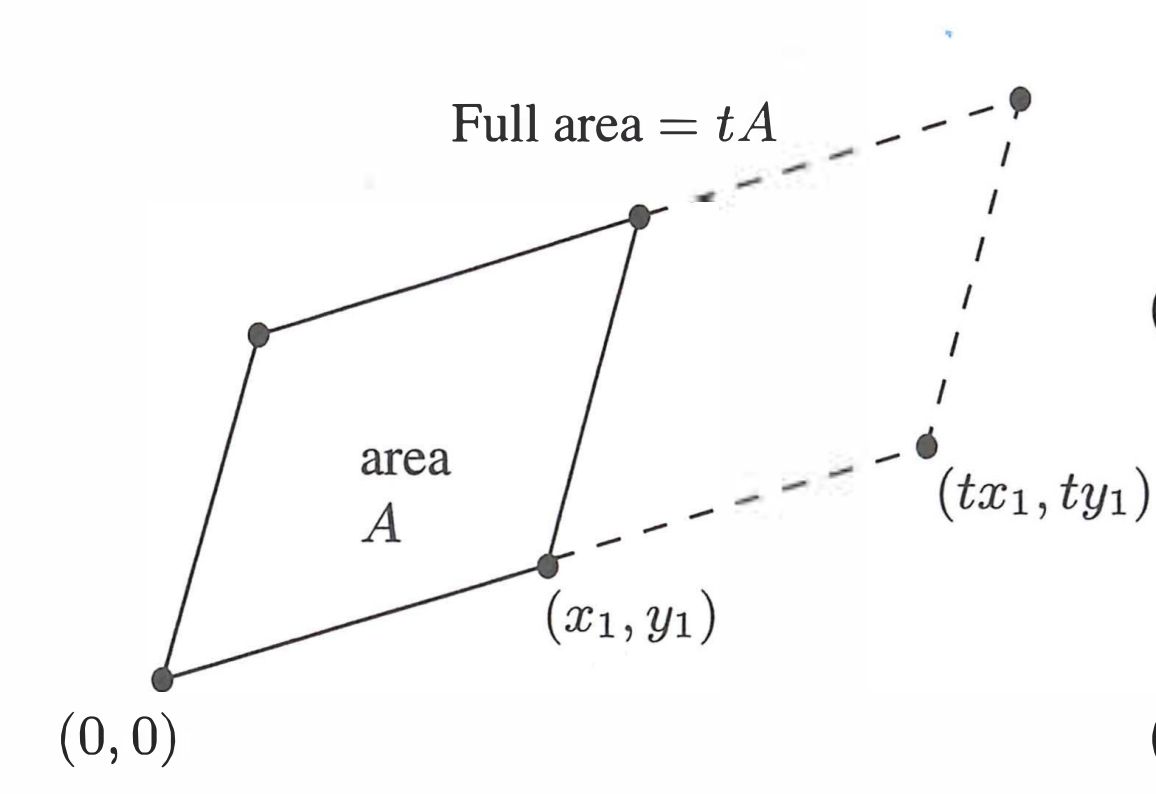
[3] If row 1 is multiplied by \(t\), the area is also multiplied by \(t\).
 |
|---|
| Introduction to Linear Algebra, 5th edition |
Hence, the area satisfies the properties of the determinant.
Cross Product
The cross product is a special application for three dimensions. Consider vectors \(u=(u_1,u_2,u_3)\) and \(v=(v_1,v_2,v_3)\). The cross product is a vector in three dimensions denoted by \(u \times v\).
The components of cross product are 2 by 2 cofactors.
Definition
The cross product of \(u = (u_1, u_2, u_3)\) and \(v=(v_1,v_2,v_3)\) is a vector
\[u \times v = \begin{vmatrix} i & j & k \\\ u_1 & u_2 & u_3 \\\ v_1 & v_2 & v_3\end{vmatrix} = \begin{bmatrix} u_2v_3 - u_3v_2 \\\ u_3v_1 - u_1v_3 \\\ u_1v_2 - u_2v_1 \end{bmatrix}\]This cross product \(u \times v\) is perpendicular to \(u\) and \(v\). The cross product \(v \times u = -(u \times v)\).
Length of Cross Product
\[\lVert u \times v \rVert = \lVert u \rVert \lVert v \rVert \lvert \sin{\theta} \lvert\]Property 1
\(v \times u = -(u \times v)\) becuase it reverses two rows
Its direction is perpendicular to \(u\) and \(v\) pointing “up” or “down” by the right hand rule (from \(u\) to \(v\)).
Property 2
The cross product \(u \times v\) is perpendicular to \(u\) and \(v\).
\[u \cdot (u \times v) = u_1(u_2v_3 - u_3v_2) + u_2(u_3v_1 - u_1v_3) + u_3(u_1v_2 - u_2v_1)=0\]Property 3
The cross product of any vector with itself is \(u \times u\) = 0. This is obvious because the determinant with two equal rows is \(0\).
Cross vs Dot Product Length
\[\lVert u \times v \rVert = \lVert u \rVert \lVert v \rVert \lvert \sin{\theta} \lvert\] \[\lVert u \cdot v \rVert = \lVert u \rVert \lVert v \rVert \lvert \cos{\theta} \lvert\]Area of parallelogram
The length of \(u \times v\) equals the area of the parallelogram with sides \(u\) and \(v\).
Triple Product = Determinant = Volume
Recall \(u \times v\) is a vector so we can take its dot product with another vector \(w\). This combination produces the triple product \((u \times v) \cdot w\) which is a scalar value which is equal to the volume of the \(u,v,w\) box.
\[(u \times v) \cdot w = \begin{vmatrix} w_1 & w_2 & w_3 \\\ u_1 & u_2 & u_3 \\\ v_1 & v_2 & v_3\end{vmatrix} = \begin{vmatrix} u_1 & u_2 & u_3 \\\ v_1 & v_2 & v_3 \\\ w_1 & w_2 & w_3\end{vmatrix}\]\((u \times v) \cdot w = 0\) when \(u,v,w\) lie in the same plane
The reasons are
[1] \(u \times v\) is perpendicular to that plane so its dot product with \(w\) is zero.
[2] Three vectors in a plane are dependent. The matrix is singular (det=0)
[3] Zero volume when \(u,v,w\) box is squashed onto a plane
References
[1] Introduction to Linear Algebra, 5th edition