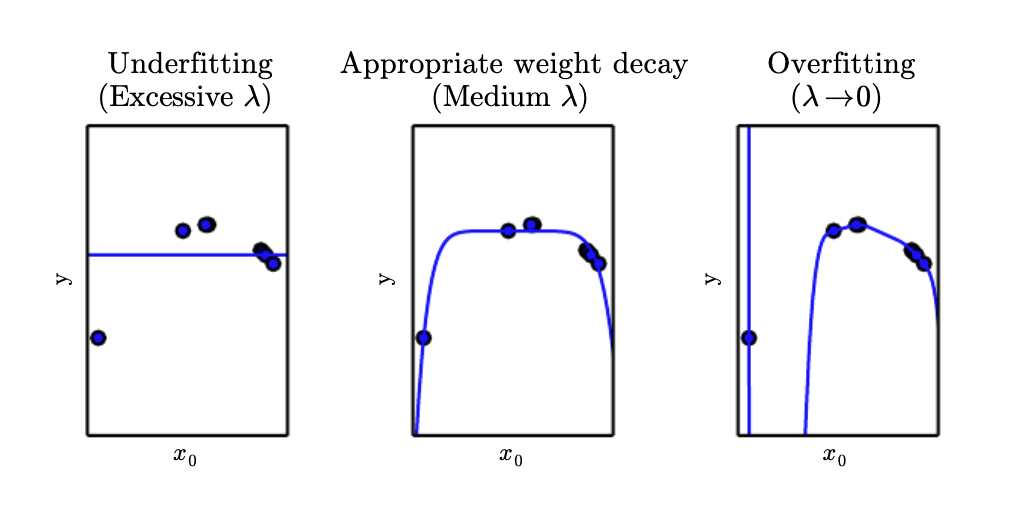
Hyperparameters
Most machine learning algorithms have hyperparamters that are not modified by the learning algorithm itself. For example, the \(\lambda\) term in the weight decay is a capacity hyperparameter that controls the strength of smaller weights. The above figure shows the effects of the various hyperparameter \(\lambda\).
Validation Set
Many times a setting is chosen to be a hyperparameter because the setting is difficult to optimize. Also, the setting must be a hyperparameter because it’s not appropriate to learn it on the training set. If it’s learned on the training set, it will be very likely to overfit only on the training set, performing worse in the test set.
To find out the optimal hyperparameters that work in the real-world, we need a validation set that the training algorithm does not encounter. It’s important that the test set must not be involved in any way during training. Therefore, the validation set must be constructed from the training set. Since the validation set is used to train the hyperparameters, the validation error will usually underestimate the generalization error.
Cross-Validation
It might be problematic to divide the dataset into a fixed training set and a fixed test set when the test set size is too small since the small test set implies uncertainty around the estimated average test error, thus not reflecting the general performance on the real-world data. Of course, if you have millions of data examlpes, it’s not a serious problem to divide into such a fixed test set.
To address this issuse, the k-fold cross validation strategy can be used where all the examples are used in the estimation of the mean test error at the cost of increased computational cost. The idea is to divide the dataset into k non-overlapping folds. For each k training processes, you use the \(k-1\) folds as the training set and the remaining one fold as test set.
References