Maximum Likelihood Estimation (MLE)
Likelihood Function
In the last post link, we’ve seen common estimators and some of their properties. But, how do we systematically choose good estimators for desired estimates? We need a principle from which we can derive specific functions that are good estimators for different models.
The most popular such principle is the maximum likelihood principle.
Consider a set of \(\)m\(\) examples \(\mathbb{X} = \{ x^{(1)},...,x^{(m)} \}\) drawn independently from the true but unknown data-generating distribution \(p_{data}(x)\). Also, let \(p_{model}(x;\theta)\) be a parametric family of probability distributions over the same spaced indexed by \(\theta\) so that \(p_{model}(x;\theta)\) maps any configuration \(x\) to a real number estimating the true probability \(p_{data}(x)\).
The likelihood function is defined by
\[\mathcal{L}\_m(\theta) = \prod\_{i=1}^m p\_{model}(x^{(i)}; \theta)\]Maximum Likelihood Estimator
Then, the maximum likelihood estimator for \(\theta\) is an estimator that maximizes the likelihood function and is defined as,
\[\theta*{ML} = \underset{\theta}{argmax} p*{model}(\mathbb{X};\theta)\] \[= \underset{\theta}{argmax} \prod*{i=1}^m p*{model}(x^{(i)};\theta) \cdots (1)\]But often times, the product over many probabilities is inconvenient. For example, it’s prone to numerical underflow and it might be hard to find the derivative. To obtain a more convenient and equivalent optimization problem, we take the logarithm of the likelihood function which transforms the product into a sum. Take the logorithm of the equation \((1)\) then we get
\[\theta*{ML} = \underset{\theta}{argmax} \sum*{i=1}^m \log p\_{model}(x^{(i)};\theta)\]Since the \(argmax\) does not change when we rescale the cost function, so we can divide it by \(m\) to obtaina version of the criterion that’s expressed as an expectation w.r.t the empirical distribution \(\hat{p}_{data}\) defined by the training data:
\[\theta*{ML} = \underset{\theta}{argmax} \mathbb{E}\_{x \sim \hat{p}*{data}} \log p\_{model}(x;\theta)\]Interpretation of MLE
Intuitive Interpretation
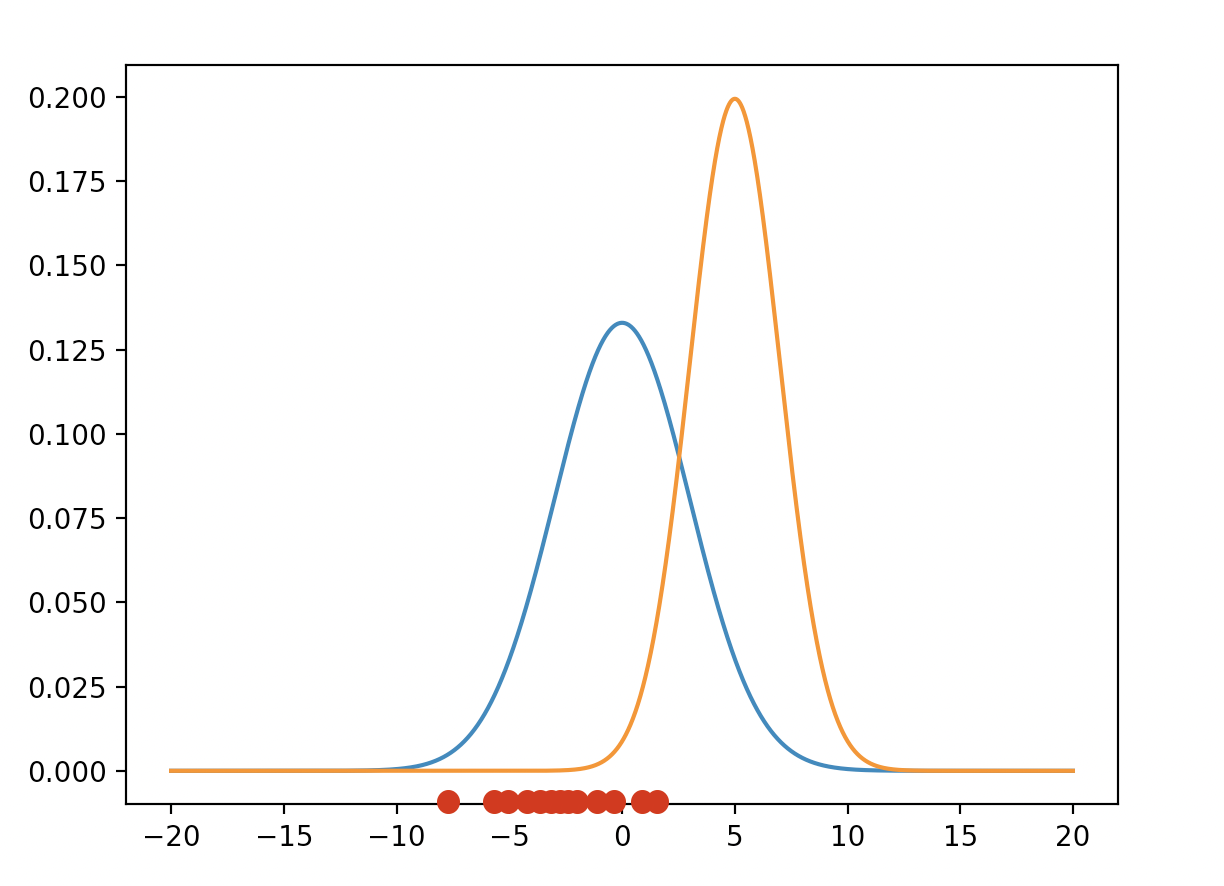
Suppose there’re two normal distributions with different \(\mu\) and \(\sigma\) parameters. Also, suppose the training data are in red-color dots. Which distribution fits more to the data? The blue curve gives a higher chance that we discovered a probability distribution that fits pretty well on our data. The product of all the corresponding y-axis for each data point or the probability, is the likelihood function. Hence, the blue curve gives a higher likelihood.
Kullback-Leibler(KL) Divergence Interpretation
One way to interpret the maximum likelihood estimation is to interpret it as minimizing the dissimilarity between the empirical distribution \(\hat{p}_{data}\) defined by the training set and the model distribution. Here, the degree of dissimilarity between the two distributions is measured by the KL divergence. The KL divergence is given by
\[D\_{KL}(\hat{p}\_{data} \lvert \rvert p\_{model}) = \mathbb{E}\_{X \sim \hat{p}\_{data}}[\log \hat{p}\_{data}(x) - \log p\_{model}(x)]\]Since the left term in the expectation is a function of the data-generating process, when we train the model to minimize the KL divergence, we only care about the right term. Therefore, we only need to minimize
\[-\mathbb{E}\_{X \sim \hat{p}\_{data}}[\log p\_{model}(x)]\]which is equivalent to maximizing the loglikelihood function.
Minimizing the KL divergence is exactly the same as minimizing the cross-entropy between the distributions. In machine learning literature, the term “cross-entropy” is used to refer to the negative log-likelihood of a Bernoulli or softmax distribution but this is incorrect. Any loss consisting of a negative log-likelihood is a cross-entropy between the empirical distribution by the training set and the probability distribution by the model.
Conditional Log-Likelihood and Mean Squared Error (MSE)
The maximum likelihood estimator can be generalized to estimate a conditional probability \(P(y \lvert x; \theta)\) to predict \(y\) given \(x\). This is very common for most supervised learning. If \(X\) represents all our inputs and \(Y\) all our targets, then the conditional maximum likelihood estimator is
\[\theta\_{ML} = \underset{\theta}{argmax}P(Y \lvert X; \theta)\]Assuming the examples are \(i.i.d\), then we can further decompose into
\[\theta*{ML} = \underset{\theta}{argmax} \sum*{i=1}^m \log P(y^{(i)} \lvert x^{(i)}; \theta)\]Linear Regression as Maximum Likelihood
Previously, we handled linear regression with an algorithm that learns a mapping from \(x\) to \(\hat{y}\) that minimizes the MSE. However, we have not justified the use of MSE. Let’s do it.
We now consider linear regression as maximum likelihood estimation problem. Instead of producing a single prediction \(\hat{y}\), we now consider the model as producing a conditional distribution \(p(y \lvert x)\). With an infinitely large training set, there might be several training examples with the same \(x\) but different \(y\). The goal of the learning algorithm is to fit the distribution \(p(y \lvert x)\) to all those different \(y\) values that are all compatible with \(x\).
Let’s define
\[p(y \lvert x) = \mathcal{N}(y; \hat{y}(x;w),\sigma^2)\]where the function \(\hat{y}(x;w)\) gives the prediction of the mean of the Gaussian. We assume that the variance \(\sigma^2\) is fixed.
Then, since the examples are assumed to be \(i.i.d.,\) the conditional log-likelihood is given by
\[\sum\_{i=1}^m \log p(y^{(i)} \lvert x^{(i)}; \theta)\] \[= \sum\_{i=1}^m \log \frac{1}{\sigma \sqrt{2\pi}} exp \left( -\frac{1}{2} \left( \frac{\hat{y}^{(i)} - y^{(i)}}{\sigma} \right)^2 \right)\] \[= \sum\_{i=1}^m -\log \sigma \sqrt{2\pi} - \frac{1}{2}\left( \frac{\hat{y}^{(i)} - y^{(i)}}{\sigma} \right)^2\] \[= \sum\_{i=1}^m -\log \sigma - \log \sqrt{2 \pi} - \frac{(\hat{y}^{(i)} - y^{(i)})^2}{2 \sigma^2}\] \[= -m\log \sigma - \frac{m}{2} \log 2\pi - \sum\_{i=1}^m \frac{\lvert \lvert \hat{y}^{(i)} - y^{(i)} \rvert \rvert^2}{2\sigma^2} \cdots (2)\]where \(\hat{y}^{(i)}\) is the output of the linear regression on the \(i^{th}\) input \(x^{(i)}\) and \(m\) is the number of the training examples. An interesting observation is that maximizing the log-liklihood with respect to \(w\) yields the same estimate of the parameters \(w\) as does miniminzing the mean squared error since all the other terms from the equation \((2)\) do not dependent on \(w\).
\[MSE = \frac{1}{m} \lvert \lvert \hat{y} - y \rvert \rvert_2^2\]Therefore, the two criteria (MSE and Conditional MSE) have different values but have the same location of the optimum. This justifies that MSE is a valid maximum likelihood estimation procedure.
Properties of Maximum Likelihood
The best advantage of the maximum likelihood estimator is that it can be shown to be the best estimator asymptotically as \(m \rightarrow \infty\).
Under appropriate conditions, the maximum likelihood estimator has the property of consistency which indicates that as \(m \rightarrow \infty\), the maximum likelihood estimate of a parameter converges to the true value of the parameter. The conditions for this property are:
The true distribution \(p_{data}\) must lie within the model family \(p_{model}(;\theta)\). Otherwise, no estimator can recover \(p_{data}\).
The true distribution \(p_{data}\) must correspond to exactly one value of \(\theta\). Otherwise, maximum likelihood can recover the correct \(p_{data}\) but will not be able to determine which value of \(\theta\) was used by the data-generating process.
There are other inductive principles besides MLE which are consistent estimators. However, consistent estimators can differ in their statistical efficiency, indiciating that one consistent estimator may obtain lower generalization error for a fixed number of examples \(m\), or may require fewer examples to obtain a fixed level of generalization error. Also, the Cramer-Rao lower bound shows that no consistent estimator has a lower MSE than the maximum likelihood estimator.
References
[1] deeplearningbook.org Ch.5