[Paper] ResNet - Deep Residual Learning for Image Recognition

ResNet

ResNet was a breakthrough idea that swept ILSVRC 2015 classication, ImageNet detection, localization and COCO detection as well as segmentation competition. Then what was special about ResNet?

What was ResNet trying to address?

Extremely deep neural networks suffer from training error. But the really weird thing is it doesn’t suffer only from the test set, but also from training set. Wait..this is quite counterintuitive. In fact, adding more and more layers lead to even higher training error. It’s no more an overfitting problem. The author of the paper conjectured that it’s harder to optimize extremely deep neural networks. The ultimate goal of ResNet is to address this very counterintuitive degradation problem.

Hypothesize that ResNet is easy to optimize and therefore able to overcome degradation problems
Enjoy extra accuracy by deeper and deeper model

Deep Residual Learning Framework

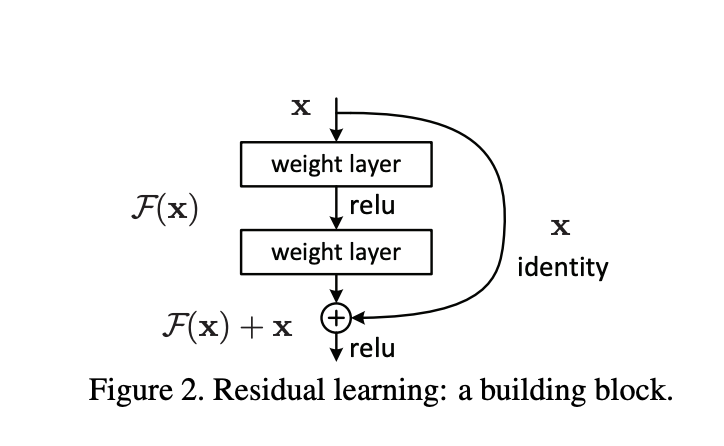
The main idea of ResNet is to fit a residual mapping rather than to fit the original desired underlying mapping. Let me elaborate.


He et al. 2015

Let \(H(x)\) be the desired underlying mapping, then instead of trying to fit \(H(x)\) directly, we try to fit \(F(x):=H(x)-x\) where x is the identity mapping. The author hypothesized that it’s easier to optimize the residual mapping than the original mapping. In the worst case scenario, if, in fact, the identity mapping were optimal, then it would be much easier to push the residual to 0(push \(F(x)\) to 0) than to fit an identity mapping by learning a stack of nonlinear layers. To achieve this mapping, shortcut connection is introduced which is simpling “copying” \(x\) and add to \(F(x)\).

Intuition for shortcut connection

Why might this “shortcut connection” be helpful? The intuition is that if the “plain” nonlinear layers can asymptotically approximate the underlying function \(H(x)\), then it’s equally like that it can fit the residual function \(F(x):=H(x)-x\). Moreover, as mentioned earlier, if the identity mapping were indeed optimal, then the netowrk could push the residual to 0 to recover the identity mapping. In other words, the residual mapping must perform AT LEAST as good as the plain nonlinear layers. In the worst case scenario where all the residual mappings were actually useless, which is very unlikely to happen, the ResNet will at least do no harm to the plain nonlinear layer counterparts.

Identity mapping by shortcuts

ResNet adopts residual learning to every few stacked layers which you can think of as building block. The building block is formally defined as \(y=F(x,\{W_i\})+x\) Where \(x\) and \(y\) denote input and output of the building block and \(F(x,{W_i\})\) denotes the residual mapping. For example, in two layer block, the representation would be \(F=W_2\sigma(W_1x)\) where \(\sigma\) is ReLU nonlinearity(biases are omitted). The shortcut connection \(F+x\) is done by element-wise addition. The last nonlinearity is applied after this shortcut connection (\(i.e., \sigma(y)\)).

One of the advantages of this shorcut connection is that it introduces neither extra parameters nor computational complexity as it’s a trivial element-wise addition. Note that to perform the element-wise addition, the dimensions of \(F\) and \(x\) must be equal. However, if this is not the case, the dimensions could be matched by two options.

The shortcut is applied with zero-padding to increase dimension(no extra parameter)
The linear projection \(W_s\) (1x1 conv) is performed by the shortcut connection: \(y=F(x,W_i)+W_sx\)

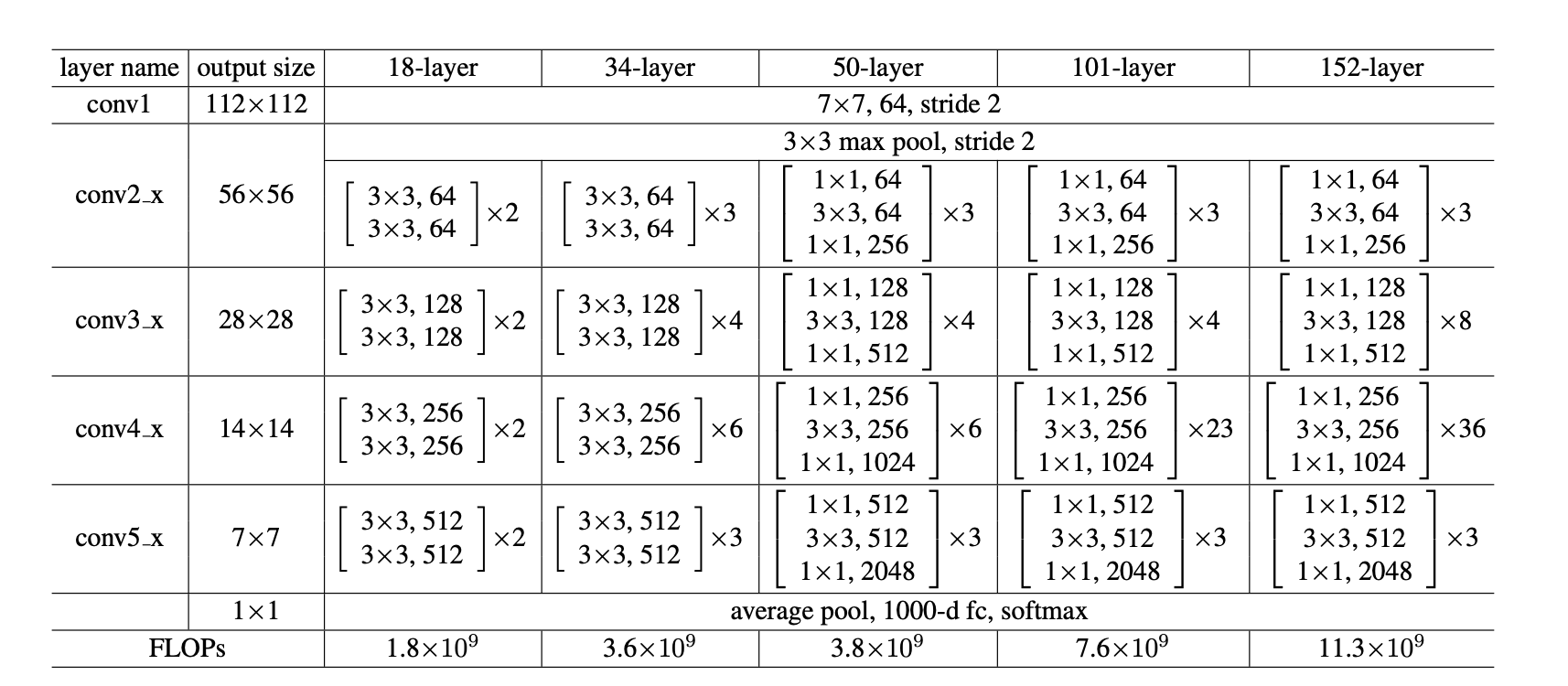
Network Architecture

The base architecture resembles VGGNet.


He et al. 2015

3x3 filter
Downsample by conv layer with stride of 2 instead of maxpooling.
Global average pooling after Conv layer and before classifiers.
1000 ouput classes with osftmax function.
Batch normalization after each conv layer.
SGD with momentum of 0.9
Mini batch size of 256
Initial learning rate is 0.1 which gets divided by 10 when plateaus.
Weight decay of 0.0001.
No dropout
In testing, 10-crop average testing.

Performance

Despite the significant increase of depth, ResNet has much more efficient memory usage and better performance.


He et al. 2015

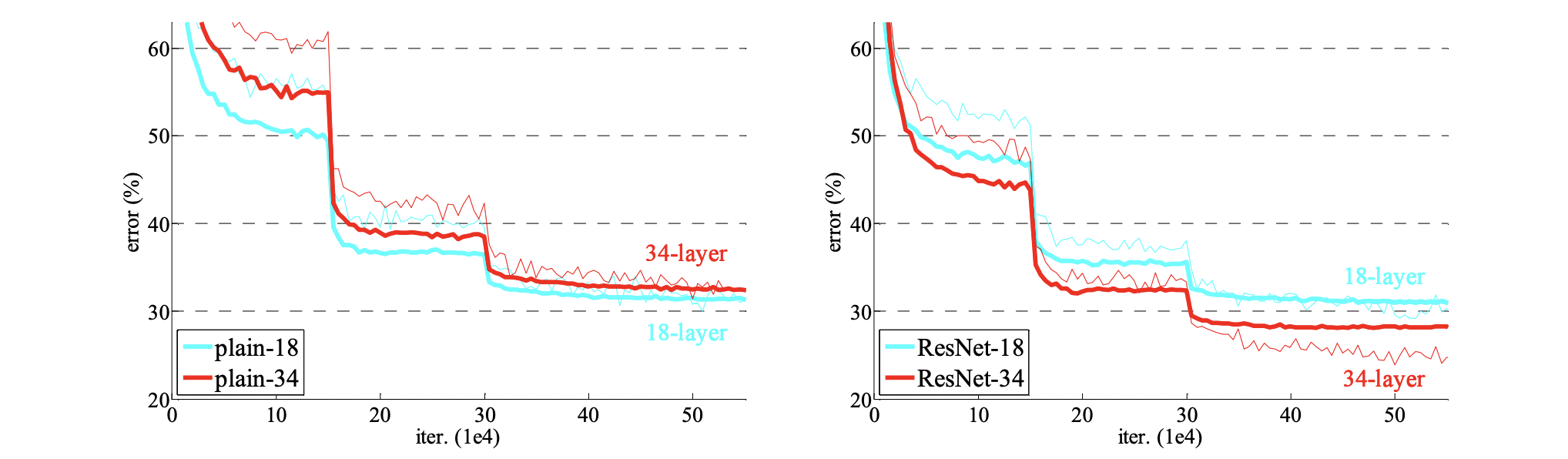
For explicit comparision, the experiment was performed for plain network and residual network with exact same number of parameters(of course, except the shortcuts). The left graph in the figure shows that the plain 34-layer network shows higher validation error than the shallower 18-layer(degradation). However, the equivalent counterpart, ResNet-34 indeed outperforms ResNet-18. The result expliclty hits that the residual mapping indeed seems to address the degradation problem.


He et al. 2015

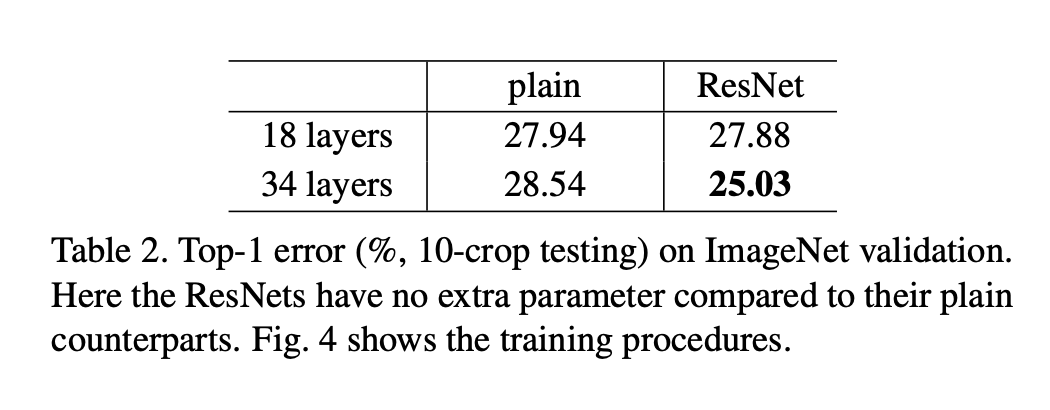
Table 2 gives another explicit comparison of plain and residual networks. ResNet-34 reduces the top-1 error by 3.5% compared to plain 34 layer counterpart.

It is also noticable that the ResNet-34 has fewer filters and lower complexity than VGGNet although there’s a huge increase of depth. The ResNet-34 has 3.6 billion FLOPs(floating-point computations) which is only 18% of VGG-19 which has 19.6 billion FLOPs.


He et al. 2015

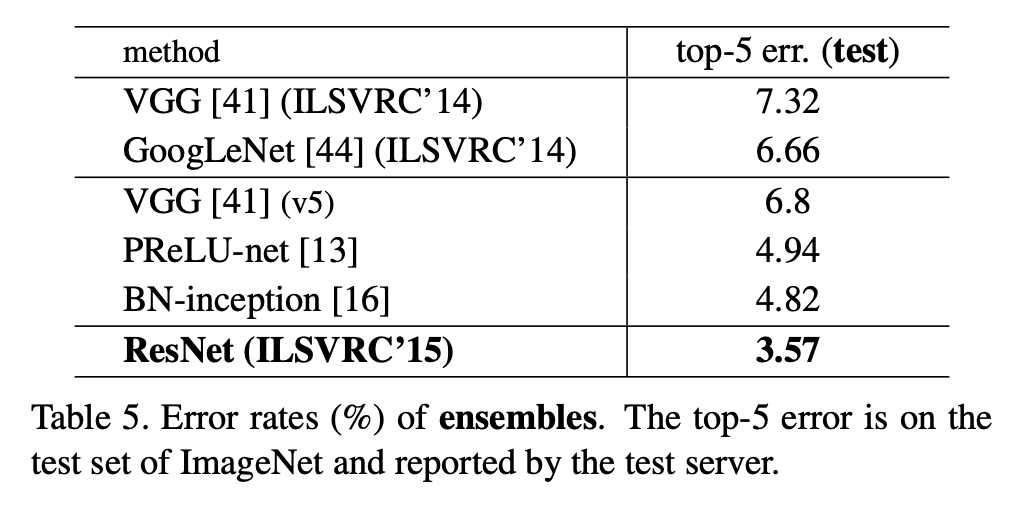
ResNet also achieves wonderful ensemble performance.

Bottleneck Architectures

You might have noticed that ResNet-50 and above have two 1x1 conv filters in the building block. To achieve affordable computational efficiency, the building block is modified as a bottleneck design. Instead of feeding the huge complexity to the 3x3 conv layer, 1x1 conv layers reduce and then increase(restoring) the dimension, taking burdens away from 3x3 layer. Indeed, the 50/101/152-layer ResNets are recorded more accurate than the shallower Resnet by considerable margins with no degradation problem. The model also has great generalization performance where it could be applied to object detection and segmentation problems.

Pytorch Implementation

  
import torch
import torch.nn as nn
from typing import List

class Bottleneck(nn.Module):
    expansion = 4

    def __init__(self, in_channels, block_channels, identity_downsample = None, stride = 1):
        super(Bottleneck, self).__init__()
        self.in_channels = in_channels
        self.block_channels = block_channels
        self.identity_downsample = identity_downsample
        self.stride = stride

        self.conv1x1_1 = nn.Sequential(
            nn.Conv2d(in_channels, block_channels, 1, stride=1, padding=0, bias=False),
            nn.BatchNorm2d(block_channels),
            nn.ReLU()
        )

        self.conv3x3 = nn.Sequential(
            nn.Conv2d(block_channels, block_channels, 3, stride=stride, padding=1, bias=False),
            nn.BatchNorm2d(block_channels),
            nn.ReLU()
        )

        self.conv1x1_2 = nn.Sequential(
            nn.Conv2d(block_channels, block_channels * self.expansion, 1, stride=1, padding=0, bias=False),
            nn.BatchNorm2d(block_channels * self.expansion)
        )
        self.relu = nn.ReLU()

    def forward(self, x):
        identity = x.detach().clone()
        x = self.conv1x1_1(x)
        x = self.conv3x3(x)
        x = self.conv1x1_2(x)

        if self.identity_downsample is not None:
            identity = self.identity_downsample(identity)

        x += identity
        x = self.relu(x) # Apply ReLU after shortcut
        return x



class ResNet(nn.Module):
    def __init__(self, block: Bottleneck, layers: List[int], in_channels = 3, num_classes = 1000):
        super(ResNet, self).__init__()
        self.in_channels = in_channels
        self.num_classes = num_classes

        # [1] conv1
        self.conv1 = nn.Sequential(
            nn.Conv2d(in_channels, 64, kernel_size=7, stride=2, padding=3),
            nn.BatchNorm2d(64),
            nn.MaxPool2d(3, stride=2)
        )
        self.in_channels = 64

        # [2] conv2_x, 3_x, 4_x, 5_x
        self.conv2_x = self._make_layer(block, layers[0], block_channels = 64, stride = 1)
        self.conv3_x = self._make_layer(block, layers[1], block_channels = 128, stride = 2)
        self.conv4_x = self._make_layer(block, layers[2], block_channels = 256, stride = 2)
        self.conv5_x = self._make_layer(block, layers[3], block_channels = 512, stride = 2)

        # [3] classifiers
        self.classifiers = nn.Sequential(
            nn.AdaptiveAvgPool2d((1,1)),
            nn.Flatten(),
            nn.Linear(2048, num_classes)
        )

    def _make_layer(self, block, num_blocks, block_channels, stride):
        identity_downsample = None
        layers = []

        if stride != 1 or self.in_channels != 4 * block_channels:
            identity_downsample = nn.Sequential(
                nn.Conv2d(self.in_channels, 4 * block_channels, kernel_size=1, stride=stride, bias=False), # linear projection
                nn.BatchNorm2d(4 * block_channels)
            )

        # This connects between the final ouput of previous bottleneck to the input of the current bottleneck
        # The reason we do this is that the input of bottleneck might come from TWO paths
            # 1. Previous bottleneck (if current is conv3_x, then from conv2_x). In this case,
            # input size of conv1x1 of conv3_x(128)  is HALF of final output of conv2_x(256)
            # 2. bottleneck uses expansion of 4. Denoting current bottleneck's channels for 1x1, 3x3, 1x1 as p,p,4p,
            # the input channel would be 4p -> 1p.
            # Therefore, we must separate the very first(from ANOTHER bottleneck) bottleneck and
            # simply from the CURRENT repetitive bottleneck
        layers.append(
            Bottleneck(self.in_channels, block_channels, identity_downsample, stride=stride)
        )

        #4p -> p. Like a recursion, we're going back to the beginning of current bottleneck
        self.in_channels = block_channels * 4

        for _ in range(1, num_blocks):
            layers.append(
                Bottleneck(self.in_channels, block_channels, stride=1) # no identity downsample
            )

        return nn.Sequential(*layers)

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2_x(x)
        x = self.conv3_x(x)
        x = self.conv4_x(x)
        x = self.conv5_x(x)
        x = self.classifiers(x)
        return x


# Testing
resnet = {
    'resnet50': [3, 4, 6, 3],
    'resnet101': [3, 4, 23, 3],
    'resnet152': [3, 8, 36, 3]
}

d = torch.randn(1,3,224,224)

model = ResNet(Bottleneck, resnet['resnet50'])

def print_layer_shape_hook(module, input, output):
    print("-"*80)
    print(module)
    print(f"[input] {input[0].shape}")
    print(f"[ouput] {output.shape}")

for name, submodule in model.named_modules():
    if isinstance(submodule, (nn.Conv2d, nn.MaxPool2d, nn.Linear, nn.AdaptiveAvgPool2d)):
        submodule.register_forward_hook(print_layer_shape_hook)

_ = model(d)

Shape of each layer

Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3)) [input] torch.Size([1, 3, 224, 224]) [ouput] torch.Size([1, 64, 112, 112])

MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False) [input] torch.Size([1, 64, 112, 112]) [ouput] torch.Size([1, 64, 55, 55])

Conv2d(64, 64, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 64, 55, 55]) [ouput] torch.Size([1, 64, 55, 55])

Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False) [input] torch.Size([1, 64, 55, 55]) [ouput] torch.Size([1, 64, 55, 55])

Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 64, 55, 55]) [ouput] torch.Size([1, 256, 55, 55])

Conv2d(256, 64, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 256, 55, 55]) [ouput] torch.Size([1, 64, 55, 55])

Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False) [input] torch.Size([1, 64, 55, 55]) [ouput] torch.Size([1, 64, 55, 55])

Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 64, 55, 55]) [ouput] torch.Size([1, 256, 55, 55])

Conv2d(256, 64, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 256, 55, 55]) [ouput] torch.Size([1, 64, 55, 55])

Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False) [input] torch.Size([1, 64, 55, 55]) [ouput] torch.Size([1, 64, 55, 55])

Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 64, 55, 55]) [ouput] torch.Size([1, 256, 55, 55])

Conv2d(256, 128, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 256, 55, 55]) [ouput] torch.Size([1, 128, 55, 55])

Conv2d(128, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False) [input] torch.Size([1, 128, 55, 55]) [ouput] torch.Size([1, 128, 28, 28])

Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 128, 28, 28]) [ouput] torch.Size([1, 512, 28, 28])

Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False) [input] torch.Size([1, 256, 55, 55]) [ouput] torch.Size([1, 512, 28, 28])

Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 512, 28, 28]) [ouput] torch.Size([1, 128, 28, 28])

Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False) [input] torch.Size([1, 128, 28, 28]) [ouput] torch.Size([1, 128, 28, 28])

Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 128, 28, 28]) [ouput] torch.Size([1, 512, 28, 28])

Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 512, 28, 28]) [ouput] torch.Size([1, 128, 28, 28])

Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False) [input] torch.Size([1, 128, 28, 28]) [ouput] torch.Size([1, 128, 28, 28])

Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 128, 28, 28]) [ouput] torch.Size([1, 512, 28, 28])

Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 512, 28, 28]) [ouput] torch.Size([1, 128, 28, 28])

Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False) [input] torch.Size([1, 128, 28, 28]) [ouput] torch.Size([1, 128, 28, 28])

Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 128, 28, 28]) [ouput] torch.Size([1, 512, 28, 28])

Conv2d(512, 256, kernel_size=(1, 1), stride=(1, 1), bias=False) [input] torch.Size([1, 512, 28, 28]) [ouput] torch.Size([1, 256, 28, 28])

Conv2d(256, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False) [input] torch.Size([1, 256, 28, 28]) [ouput] torch.Size([1, 256, 14, 14])