Introduction
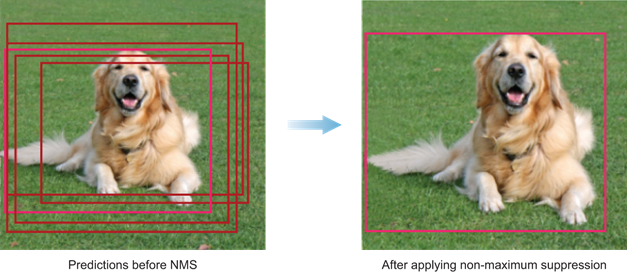
When real-time inference is not required, ensembling different models can bring about performance boost. Some of popula ensembling methods for object detection include non-maximum suppression which simply removes “duplicated” bounding boxes whose IoU with a selected bounding box is greater than the given IoU threshold. Another recent method is Soft NMS which reduces the confidences of proposals propotional to IoU values. However, these methods cull out some bounding boxes based on certain criteria but do not utilize all the bounding boxes. Thus, some bounding boxes that might potentially contribute to the good performance are removed.
In this paper, a new ensembling method, weighted boxes fusion (WBF), is introduced which utilizes all proposed bounding boxes to construct the averaged boxes. The weighted boxes fusion is quite simple and straightforward yet brings about a large performance boost.
Note that the implementation in this post my own implementation which is intended to be easier and more intuitive to understand. That means it does not aim for efficiency. Once you understand how the WBF algorithm works, you can jump to the official implementation by the original author which I provided in the later section.
Non-maximum suppression (NMS)
So far, the non-maximum suppression is probably the most-known ensembling method. In NMS, first sort all the bounding boxes with respect to confidence score. Starting from the highest confidence score bounding box (Box A), all the bounding boxes whose IoU with the Box A are greater than the pre-defined IoU threshold are removed, leaving out only the “best” bounding box for a specific target object. However, setting this threshold is tricky: If there’re objects of same class side by side, then only one will be remained which is not something we want.
Soft-NMS
Instead of removing bounding boxes, soft-NMS reduces the confidences of the proposals proportional to IoU value. The soft-NMS showed a noticeable improvement over the plain NMS method.
However, both NMS and soft-NMS discard redundant boxes so they cannot produce averaged localization predictions from different models effectively.
To address these issues, let’s look at how WBF works.
Weighted Boxes Fusion (WBF)
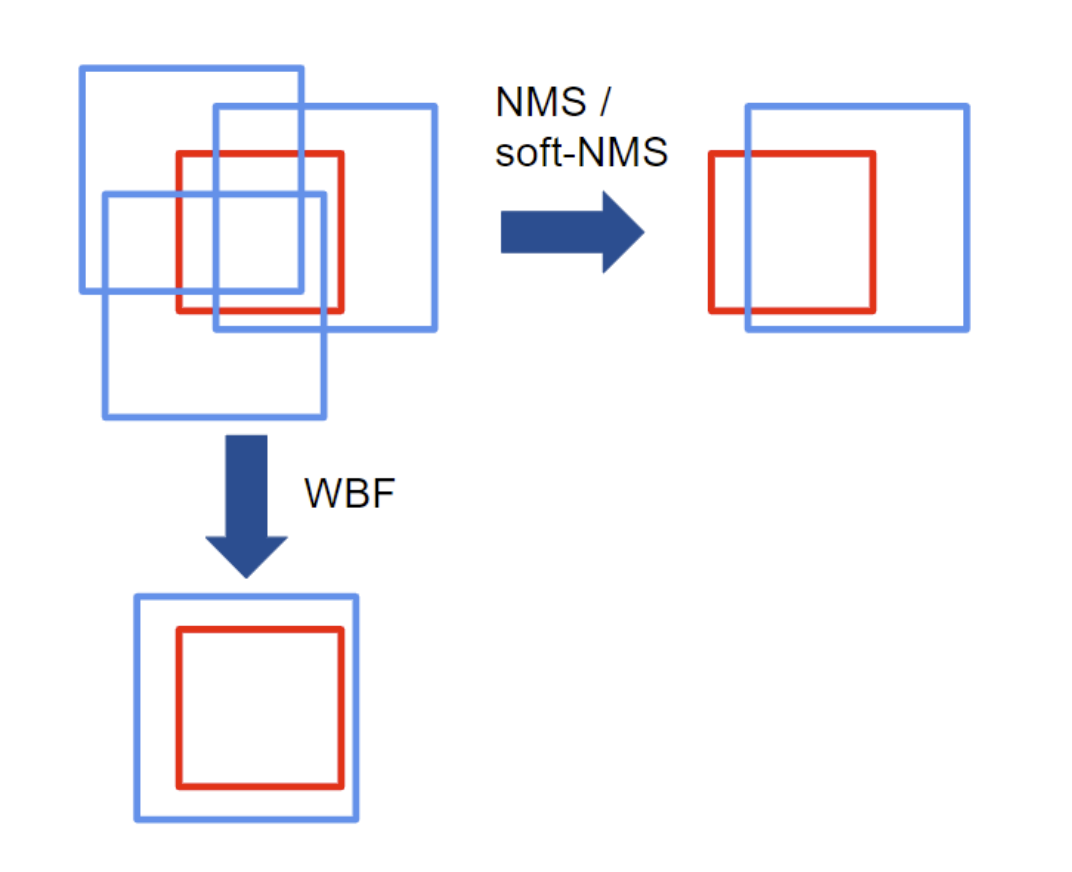
Unlike NMS and soft-NMS that discard redundant boxes, WBF algorithm makes them to all contribute to the final prediction proportionally to their confidence score. Intuitively, this is quite a fair method since unless the predicted bounding box is a really terrible prediction (e.g. confidence = 0.001), some features of that prediction must contribute to the prediction at least a bit. The difference between the NMS/Soft-NMS and the WBF is illustrated in the above figure.
Let’s now dive deep into the details of the WBF algorithm.
Full Implementation
The full implementation is given before explaining specific steps. Refer back to this implementation for each step.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
# Presets
boxes_list = [
[
[15, 30, 52, 140],
[34, 20, 78, 130],
],
[
[30, 45, 68, 140],
[25, 5, 64, 110],
]
]
for model_boxes in boxes_list:
for box in model_boxes:
box[0] /= 144.
box[1] /= 144.
box[2] /= 144.
box[3] /= 144.
scores_list = [[0.98, 0.78], [0.86, 0.82]]
labels_list = [[1, 1],[1, 1]]
weights=[1,1]
iou_thr = 0.3
skip_box_thr = 0.01
# IoU
def intersection_over_union(box1, box2):
box1_xmin, box1_ymin, box1_xmax, box1_ymax = box1[0], box1[1], box1[2], box1[3]
box2_xmin, box2_ymin, box2_xmax, box2_ymax = box2[0], box2[1], box2[2], box2[3]
inter_xmin = max(box1_xmin, box2_xmin)
inter_ymin = max(box1_ymin, box2_ymin)
inter_xmax = min(box1_xmax, box2_xmax)
inter_ymax = min(box1_ymax, box2_ymax)
intersection = max(0,(inter_xmax - inter_xmin)) * max(0,(inter_ymax - inter_ymin))
union = (
(box1_xmax - box1_xmin) * (box1_ymax - box1_ymin)
+ (box2_xmax - box2_xmin) * (box2_ymax - box2_ymin)
- intersection
)
return intersection / (union + 1e-6)
# WBF
def wbf(boxes_list, scores_list, labels_list, weights=None, iou_thr=0.5, skip_box_thr=0.05):
N = len(boxes_list)
# [1-1] Single list B
B = [box for model_boxes in boxes_list for box in model_boxes]
C = [score for model_scores in scores_list for score in model_scores]
labels = [label for model_labels in labels_list for label in model_labels]
# [1-1] Sort in decreasing order of the confidence scores C
B = sorted(zip(labels,C,B), key=lambda x: x[1], reverse=True)
for idx, b in enumerate(B):
B[idx] = list(b)
# [2] Declare empty lists: L for box clusters, F for fused boxes
L = []
F = []
# [3] Iterate through B in a cycle and try to find a matching box in F. (IoU > iou_thr)
for b_idx, b_box in enumerate(B):
best_f_idx = -1
best_iou = -1
for f_idx, f_box in enumerate(F):
iou = intersection_over_union(b_box[2], f_box[2])
if iou > best_iou:
best_iou = iou
best_f_idx = f_idx
# [4] Match Not Found
if best_iou <= iou_thr: # best_iou <= iou_thr
L.append([b_box])
F.append(b_box)
# [5] Match Found: add b_box to L at position pos corresponding to the matching box in F
else if best_iou > iou_thr:
L[best_f_idx].append(b_box)
# [6] Perform WBF
cum_C = 0.
cum_xmin = 0.
cum_ymin = 0.
cum_xmax = 0.
cum_ymax = 0.
for l_box in L[best_f_idx]:
l_label, l_conf, (xmin, ymin, xmax, ymax) = l_box
cum_C += l_conf
cum_xmin += l_conf * xmin
cum_ymin += l_conf * ymin
cum_xmax += l_conf * xmax
cum_ymax += l_conf * ymax
T = len(L[best_f_idx])
new_C = cum_C / T
new_xmin = cum_xmin / cum_C
new_ymin = cum_ymin / cum_C
new_xmax = cum_xmax / cum_C
new_ymax = cum_ymax / cum_C
F[best_f_idx] = [f_box[0], new_C, [new_xmin, new_ymin, new_xmax, new_ymax]]
# [7] After all boxes in B are processed, Re-scale confidence scores of F
for idx, f_box in enumerate(F):
T = len(L[idx])
F[idx][1] *= (min(T,N) / N)
return F
# WBF
for model_boxes in boxes_list:
for box in model_boxes:
box[0] /= 144.
box[1] /= 144.
box[2] /= 144.
box[3] /= 144.
ensembled_boxes = wbf(boxes_list, scores_list, labels_list, iou_thr=0.3, skip_box_thr=0.01)
ensembled_boxes
[Step 0] N Different Models
Suppose we have bounding boxes predictions for the same image from N different models. Alternatively, we have N predictions from the same model for the original and the augmented versions of the same image. We’ll assume the former case for now.
Construct boxes_list, scores_list, labels_list, weights. Each position of boxes_list is a list of predictions for a single model. weights parameter determines how much each model contributes to the final prediction. For simplicity, we’ll not use weights here.
Note that the box coordinates must be normalized before being processed.
Also, define the iou_thr, skip_box_thr. If a prediction has a confidence score than this skip_box_thr, then it’s not used in ensembling.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
boxes_list = [
[
[15, 30, 52, 140],
[34, 20, 78, 130],
],
[
[30, 45, 68, 140],
[25, 5, 64, 110],
]
]
scores_list = [[0.98, 0.78], [0.86, 0.82]]
labels_list = [[1, 1],[1, 1]]
weights=[1,1]
iou_thr = 0.3
skip_box_thr = 0.01
def wbf(boxes_list, scores_list, labels_list, weights=None, iou_thr=0.5, skip_box_thr=0.05):
N = len(boxes_list)
[Step 1] Merge bboxes to B
Add each predicted box from each box to a single list B. Then, it’s sorted in decreasing order of the confidence score C.
1
2
3
4
5
6
7
# [1-1] Single list B
B = [box for model_boxes in boxes_list for box in model_boxes]
C = [score for model_scores in scores_list for score in model_scores]
labels = [label for model_labels in labels_list for label in model_labels]
# [1-2] Sort in decreasing order of the confidence scores C
B = sorted(zip(labels,C,B), key=lambda x: x[1], reverse=True)
[Step 2] Boxes cluster L / Fused box F
Declare empty lists L for boxes clusters and F for fused boxes. Note that each position of L can be a set of boxes while each position of F contains only one box.
1
2
3
# [2] Declare empty lists: L for box clusters, F for fused boxes
L = []
F = []
[Step 3] Loop through B and find a match box from F
Iterate through predicted boxes in B and attempt to find a matching box in F. The matching is determined by having IoU > iou_thr. In the paper, iou_thr = 0.55 was optimal.
1
2
3
4
5
6
7
8
9
10
# [3] Iterate through B in a cycle and try to find a matching box in F. (IoU > iou_thr)
for b_idx, b_box in enumerate(B):
best_f_idx = -1
best_iou = -1
for f_idx, f_box in enumerate(F):
iou = intersection_over_union(b_box[2], f_box[2])
if iou > best_iou:
best_iou = iou
best_f_idx = f_idx
[Step 4] If no match found
If no match found, add the box from B to the end of lists L and F as new entries. Then, proceed to the next box in B (go back to [Step 3]).
If no match found for all boxes in B, the algorithm never gets to the next step.
1
2
3
4
# [4] Match Not Found
else:
L.append([b_box])
F.append(b_box)
[Step 5] If match found
If match found, add this box to the list L at the position pos corresponding to the matching box in the list F.
This indexing is ensured not to throw an error because in [Step 4], we added the box from B both to the lists L and F. Therefore, if there’s an entry in F at position pos, then it’s guaranteed that the corresponding position pos in L is not empty.
1
2
3
# [5] Match Found: add b_box to L at position pos corresponding to the matching box in F
if best_iou > iou_thr:
L[best_f_idx].append(b_box)
[Step 6] Perform WBF
Since we found a match between a box in B and a box in F at position pos, the position pos in L contains at least two boxes waiting for WBF. We now recalculate the box coordinates and confidence score in F[pos] using all T boxes accumulated in cluster L[pos]. The calculation formula is,
Although the formula might look complicated, this is in fact quite simple.
The fused confidence score is the averaged confidence of all boxes from L[pos].
The fused box coordinates are the weighted average of all boxes from L[pos] where weights are the confidence scores for the corresponding boxes. Hence, boxes with larger confidence contribute more to the fuxed box coordinates.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# [6] Perform WBF
cum_C = 0.
cum_xmin = 0.
cum_ymin = 0.
cum_xmax = 0.
cum_ymax = 0.
for l_box in L[best_f_idx]:
l_label, l_conf, (xmin, ymin, xmax, ymax) = l_box
cum_C += l_conf
cum_xmin += l_conf * xmin
cum_ymin += l_conf * ymin
cum_xmax += l_conf * xmax
cum_ymax += l_conf * ymax
T = len(L[best_f_idx])
new_C = cum_C / T
new_xmin = cum_xmin / cum_C
new_ymin = cum_ymin / cum_C
new_xmax = cum_xmax / cum_C
new_ymax = cum_ymax / cum_C
F[best_f_idx] = [f_box[0], new_C, [new_xmin, new_ymin, new_xmax, new_ymax]]
[Step 7] Re-scale confidence scores in F
After all boxes in B are processed, re-scale the confidence scores in F by multiplying by a number of boxes in a cluster and divide by a number of models N. The reason we do this is that the large number of boxes clustered together form a fused box is indicates that the fused box is predicted by many boxes, getting more weights. In simple words, if 100 boxes predict a target object A and 1 box predicts a target object B, then the former is likely to be a better prediction than the latter. The re-scaling can be done in two ways:
or
\[C = C \* \frac{T}{N}\]The author suggests the first is slightly better although not significant.
1
2
3
4
# [7] After all boxes in B are processed, Re-scale confidence scores of F
for idx, f_box in enumerate(F):
T = len(L[idx])
F[idx][1] *= (min(T,N) / N)
Result Example
1
2
3
4
5
6
# WBF
ensembled_boxes = wbf(boxes_list, scores_list, labels_list, iou_thr=0.3, skip_box_thr=0.01)
print(ensembled_boxes)
# output:
[[1, 0.8599999999999999, [0.1766795865633075, 0.1772448320413437, 0.44969315245478036, 0.9068152454780362]]]
Let’s check with the official WBF library ensemble-boxes.
1
2
3
4
5
6
7
from ensemble_boxes import *
boxes, scores, labels = weighted_boxes_fusion(boxes_list, scores_list, labels_list, iou_thr=0.3, skip_box_thr=0.01)
print(boxes)
# output:
array([[0.17667958, 0.17724484, 0.44969317, 0.90681523]])
We can see that the results are indeed the same.
[NOTE] For easier understanding, I assumed that there’s only one label in the examples. For most cases with multiple labels, we simply perform WBF for each label. Also, my implementation is not optimal. For faster algorithms, it’s highly recommended to reference the official implementation Official Implemenation Link which exploits efficient matrix calculation and numpy operations. Lastly, I also didn’t take skip_box_thr and weights into account which are implemented in the official implementation.
Visualization
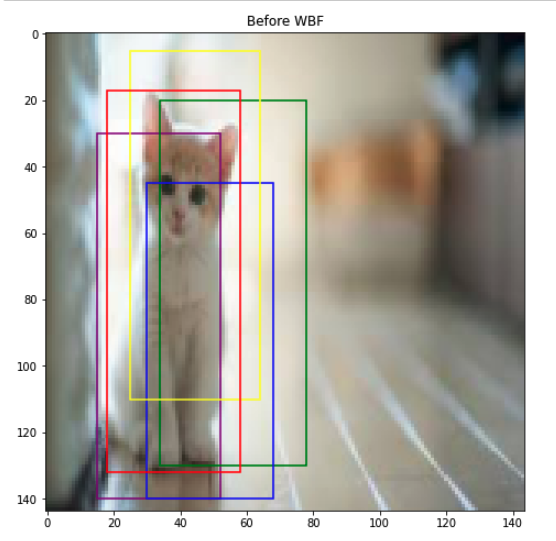
Let’s visualize our ensembled boxes using WBF. The red box refers to the ground-truth box for the cat object. The 4 predictions are ensembled and averaged to form the fused box colored in orange. It seems the fused box is a more accurate prediction than any of the original predictions.
Performance
Ensemble of two different models
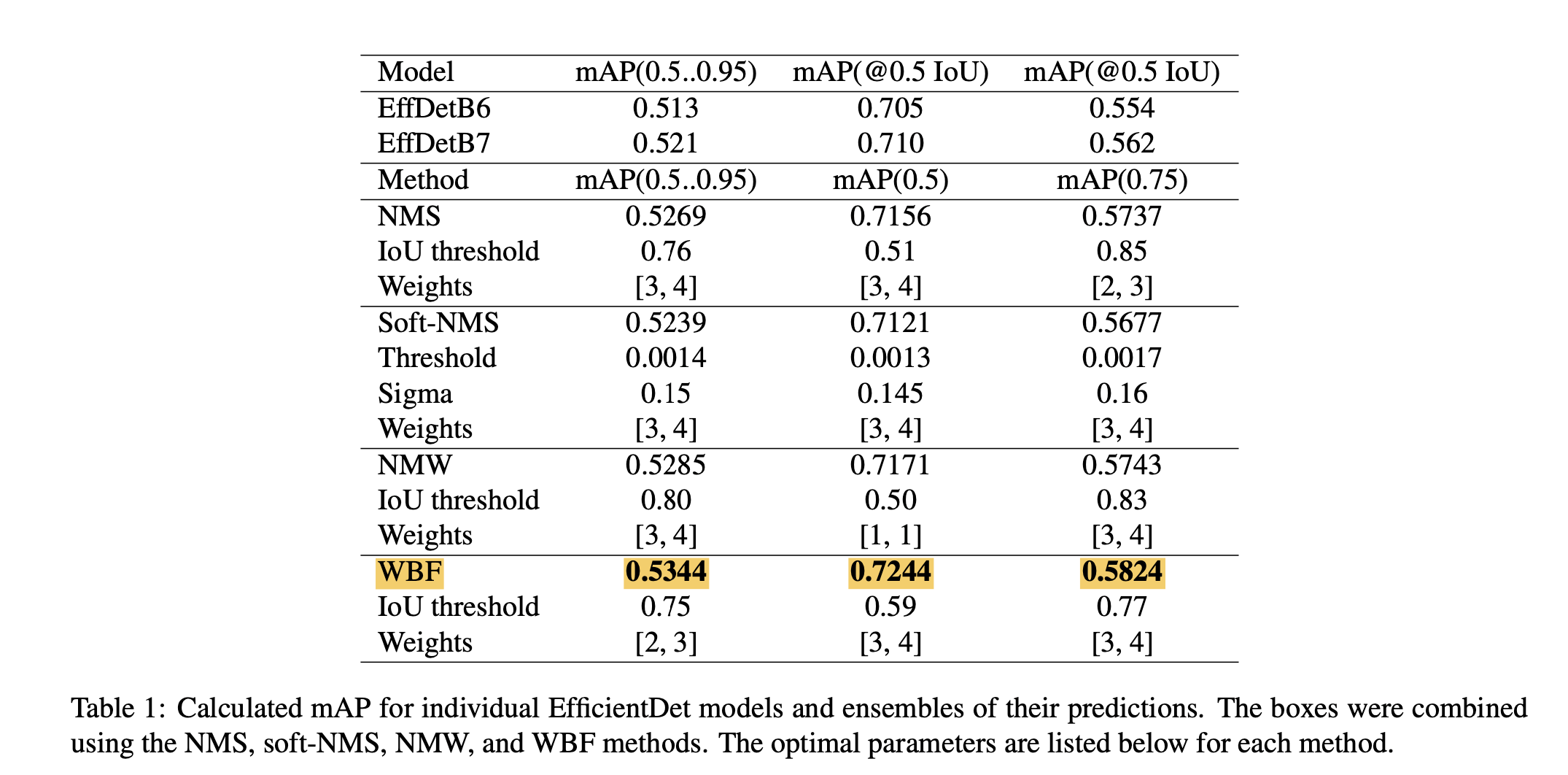
The below figure shows the performance comparison for ensembling EfficientDetB6 and EfficientDetB7. The weighted boxes fusion ensemble shows the best performance compared to other methods for all criteria.
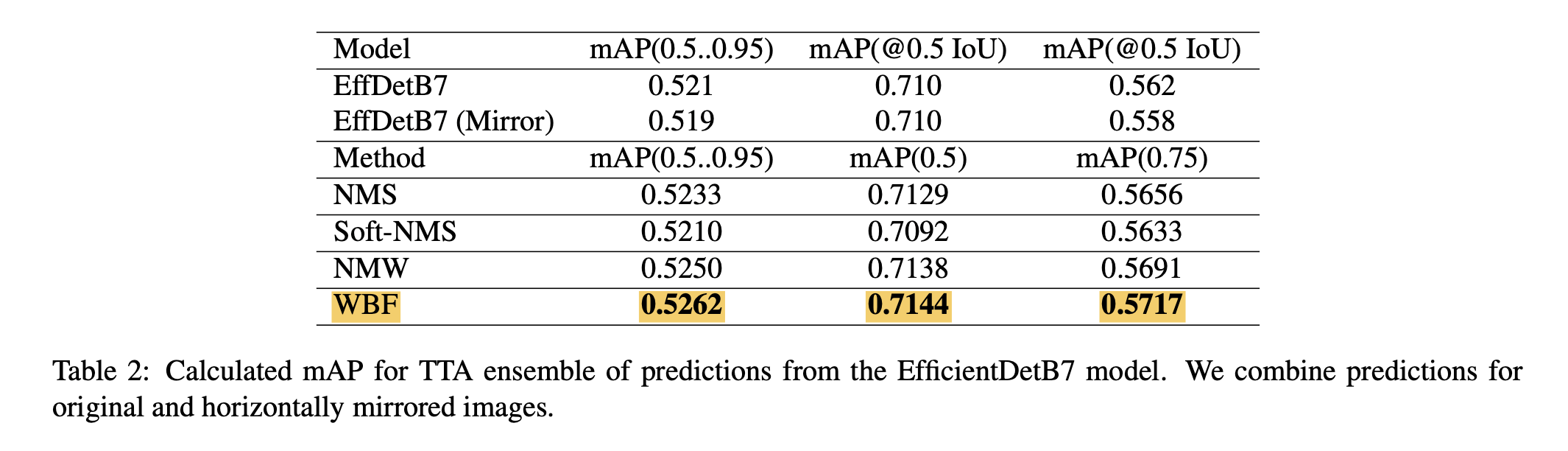
Ensemble of same models with TTA
The below figure shows the performance comparison for ensembling same models with test-time augmentation (TTA). The result shows that the WBF shows the best performance for all criteria. However, the performance boost is not that significant (~0.001-2)
Ensemble of fairly different models
The below figure shows the performance comparison for ensembling many different models with different characteristics. The result shows that the WBF shows a significant performance boost compared to other methods like NMS, soft-NMS, and NMW.
References
[1] https://arxiv.org/pdf/1910.13302.pdf
[2] https://github.com/ZFTurbo/Weighted-Boxes-Fusion