1. Web Caching
Web Caching
- Web 사용자에 의해 빈번히 요청되는 데이터를, 사용자와 지리적으로 가까운 web cache server에 보관해, 빠른 서비스를 가능하게 하는 기법
- 웹캐싱 기법의 사용 위치
- Web server
- Web user
- Proxy server
- 일개 그룹의 웹 사용자에 대한 서비스 지연시간을 줄이기 위해 사용
- 궁극적으로 network의 대역폭 절약과 함꼐 web server의 부하를 줄이는 역할도 담당
- 일개 그룹에 속한 seb server의 객체들을 캐싱하여, 서버의 부하를 줄여 결국 웹 사용자의 지연시간을 감축
Cache Replacement Algorithm
- Caching 성능에 있어 중요한 역할을 하는 알고리즘
- 전통적인 LRU 방법도 있지만, web cache는 일반적인 캐싱과는 다른 특징이 존재해서 다른 방식으로도 폭넓게 연구되었다.ㄷㄷ
- Consistency Policy
- 캐싱된 웹 객체는, 근원지 서버에서 변경될 수 있으므로, 보통 일관성 유지기법을 필요로 한다. (서버에서 데이터가 바꼈는데 캐시에서는 그대로 있으면 안될것이다)
- 하지만, 전통적인 컴퓨터 시스템이 cache consistency를 유지하지 못하면 큰 일이 나지만, 웹 캐시에서는 일관성 유지 여부가 큰 문제점을 야기하지는 않는다.
2. Web Cache Replacement Algorithm
| 캐싱방법 | 특징 | 캐싱 목표 |
|---|---|---|
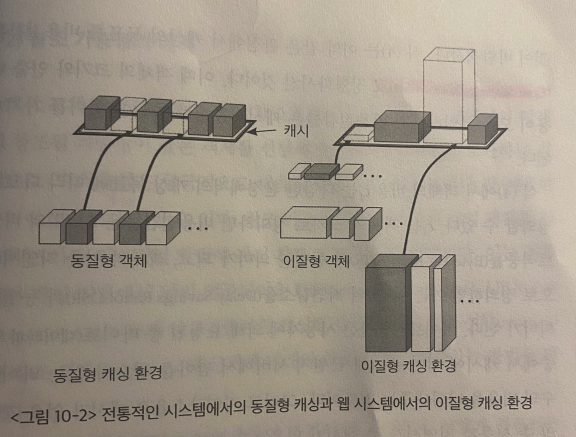
| 전통적 캐싱 | 객체들의 크기와 인출 비용이 동일 | Cache Hit Rate을 높히는 것 |
| 웹 캐싱 | 객체들의 크기와 인출 비용이 동일 X | 객체들의 참조 가능성과 이질성을 함께 고려해 다방면적 목표 |
Web caching에서는, 객체들의 크기와 인출 비용이 균일하지 않기 때문에, 객체들의 참조 가능성과 이질성읠 함께 고려해서 객체들의 가치를 평가하는게 바람직하다.
1) Web Cache의 성능평가 척도
\[\text{(1) Cache hit rate}= \sum{h_i} / \sum{r_i}\] \[\text{(2) Byte hit rate}= \sum{s_i \cdot h_i} / \sum{s_i \cdot r_i}\] \[\text{(3) Delay Savings ratio (지연감소율)}= \sum{d_i \cdot h_i} / \sum{d_i \cdot r_i}\] \[\text{(4) Cost-Saving ratio (비용절감률)}= \sum{c_i \cdot h_i} / \sum{c_i \cdot r_i}\]- $h_i$: 객체 i의 캐시적중 횟수
- $r_i$: 객체 i의 총 참조 횟수
- $s_i$: 객체 i의 크기
- $d_i$: 객체 I의 근원지 서버로부터의 인출 지연시간
- $c_i$: 객체 i의 인출 비용
2) 참조 가능성의 예측
Cache replacement algorithm은 미래의 참조를 얼마나 잘 예측하는가에 좌우된다.
일반적으로, 과거 참조 기록에 의한 방법이다.
- 전통적으로 LRU, LFU 등의 알고리즘처럼 객체는 최근 참조 성향(recency)와 참조 빈도(frequency)에 근거에 미래의 참조 성향을 예측한다.
| 교체 알고리즘 | 동작 | 단점 | 단점 예시 |
|---|---|---|---|
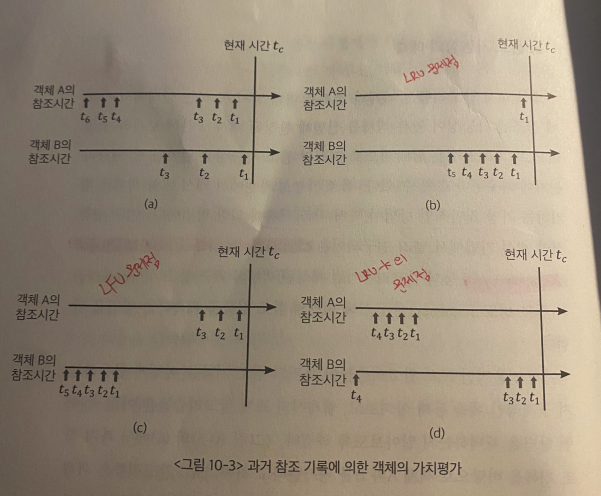
| LRU | 최근에 참조된 객체에 높은 가치부여 | 자주 참조되는 객체를 구분 X | (b)에서 문제점 |
| LFU | 더 많이 참조된 객체에 높은 가치부여 | 최근성을 구분 X (이제 막 인기를 얻는) | (c)에서 문제점 |
| LRU-K | 최근 k번쨰 참조된 시간 기준으로 가치 평가 | (d)에서 문제점 |
이러한 문제점들을 해결하기위해 LRFU (Least Recently Frequently Used)이 고안됐다.
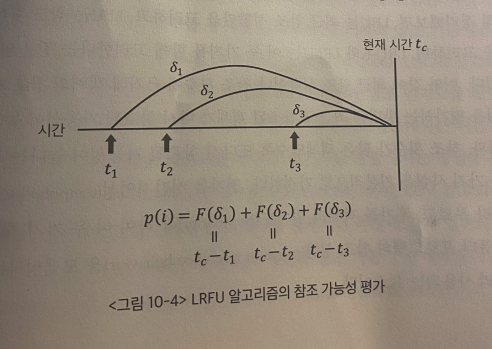
- 각각의 참조 시점을, 그 최근성에 근거해 고려한다.
- 즉, 과거 시점에서의 각각의 참조가 현재 객체의 참조 가능성을 예측하는데 기여하며, 최근의 참조일수록 기여도를 더 높게 판단한다.
| 수식 | 의미 |
|---|---|
| $p(i)$ | 객체 $i$의 참조 가능성 (모든 과거 참조시점과 참조횟수를 다 이용한다) |
| $F(x)$ | $x$시간 이전의 참조의 가치 기여도 |
\[p(i) = \sum_{k=1}^{n} F(t_c - t_k)\]
- 현재 시각 $t_i$, 객체 $i$가, 캐시에 들어온 후, $n$번이 참조되었으며, 각각의 참조 시점이 $t_1, t_2, …, t_n$이라고 가정
- $\lambda = 1$
- LRU와 동일
- 가장 최근에 참조 한번에 의한 $F(x)$값이 그 이전에 모든 참조의 가치 핪보다 크기 때문
- $\lambda = 0$
- LFU와 동일
- $F(x) = 1$이 되어 참조 횟수를 뜻하게 됨
- $0 < \lambda < 1$
- LRU와 LFU 성질 모두 가지게 됨
즉, 각 알고리즘의 특징을 정리하면
| 알고리즘 | 고려 대상 |
|---|---|
| LRU | 최근 참조 성향 |
| LFU | 참조 횟수 |
| LRU-K, LRFU | 최근 참조 성향 & 참조횟수 |
- Temporal Locality (시간지역성)
- 최근에 참조된 객체가 다시 참조될 가능성이 높은 경향
- Popularity (인기성)
- 참조 횟수가 많은 객체일수록 다시 참조될 가능성이 높은 경향
그 외 알고리즘들…
- LNC-R, LRV, MIX, GD-SIZE, LUV, etc