Introduction
Object detection task has become mature with excellent performance. Detecting a person and a cup of coffee is now a relatively easy task. However, what if the person is holding the cup of coffee? Not only localizing and classifying those objects, we also have to understand the interaction between the objects. I believe one of the crucial missions of computer vision is to understand visual perceptions.
Human-Object Interaction (HOI) detection is a task to identify “a set of interactions” in an image. Two main tasks of HOI are
localization of the subject of interaction such as humans
Classification of the interaction labels
Hence, the according output is \(<human, object, interaction>\) triplet.
Previous Works
Some of previous works treat HOI in a sequential manner where object detection is performed first, followed by associating every pair of the detected objects with a subsequent network. This is very time-consuming and requires high computation cost.
Other methods suggest parallel HOI detectors for faster inference time. These works directly localize interactions with union boxes or interaction points, thus replacing the subsequent neural network in the sequential detector. However, they predict interaction based on a simple heuristic such as distance or IoUs, yielding suboptimal performance due to hand-crafted post-processing step which requires manual threshold search.
HOTR: Human-Object interaction TRansformer
To overcome the previous drawbacks, a fast and accurate HOI model, HOTR, was proposed which predicts human-object interactions at once with a direct set prediction. HOTR utilizes transformer encoder-decoder architecture to predict HOI triplets. This architecture overcomes the previous limitations.
First, the end-to-end training step gets rid of the time-consuming hand-crafted post-processing stage. Also, the inherent nature of self-attention mechanisms of transformers extracts contextual relationships between the sub ject and the target of interactions.
HOI Detection as Set Prediction
Similar to object detection, HOTR treats object detection task as a set prediction problem that predicts localization of a human region, an object region, and multi-label classification of the interaction types.
HOTR Architecture
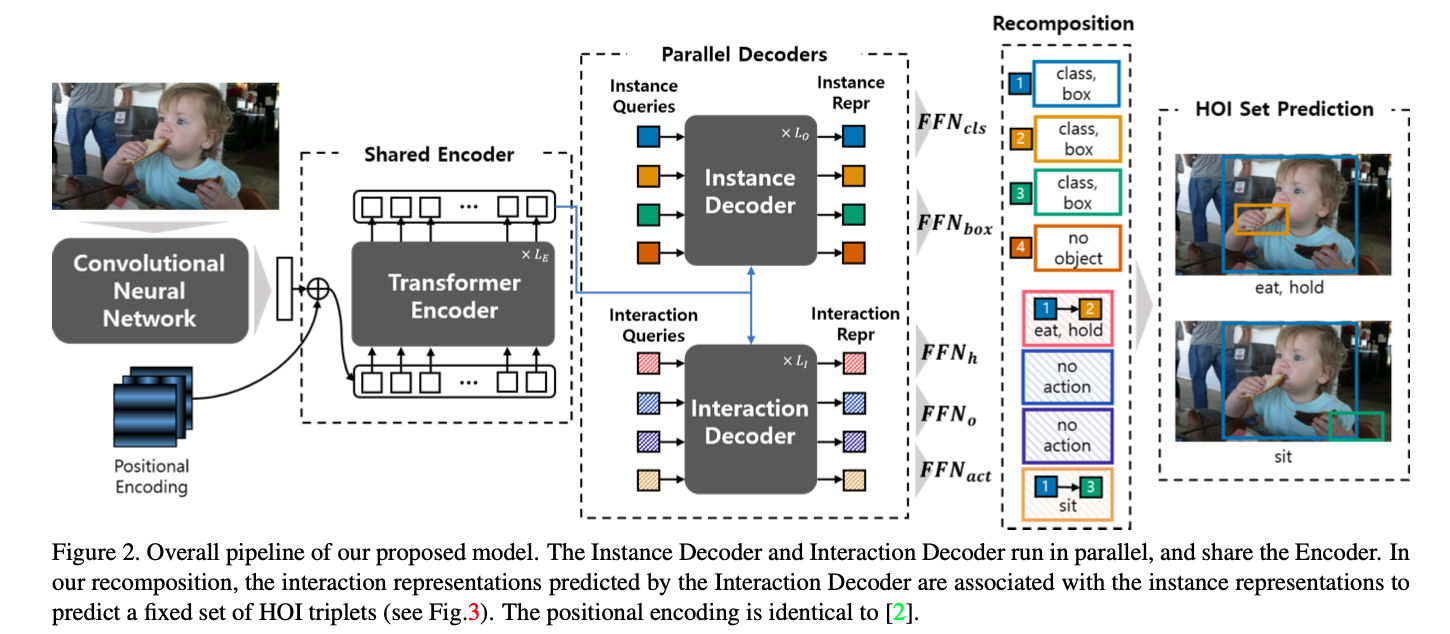
HOTR utilizes a transformer encoder-decoder architecture with a shared encoder and two parallel decodersL instance decoder and interaction decoder. Then, the proposed HO pointer associates the outputs of the two decoders to produce the final HOI triplets.
Transformer Encoder-Decoder architecture
Similar to DETR, the backbone CNN and a shared encoder extracts the global context.
Then, two sets of positional embeddings, instance queries and the interaction quries, are fed into the two parallel decoders: instance decoder and the interaction decoder. Details are shown in the figure above.
The instance decoder accepts the instance queries and transforms them to instance representations for object detection.
The interaction decoder accepts the interaction queries and transforms them to interaction representations for interaction detection.
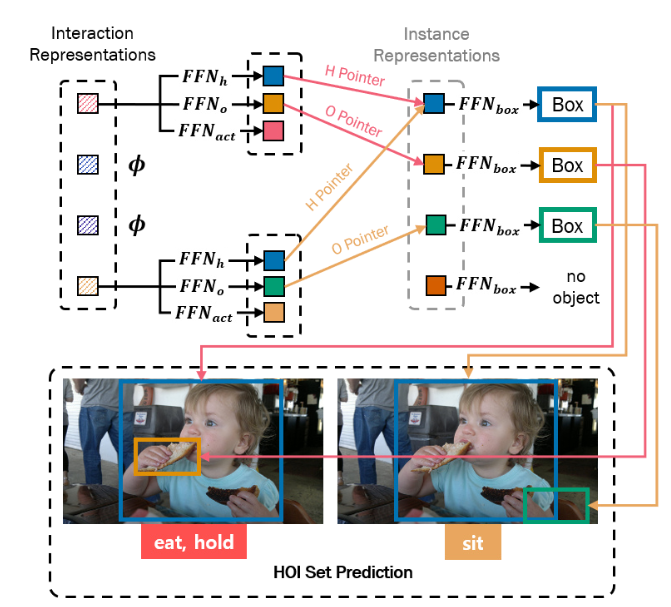
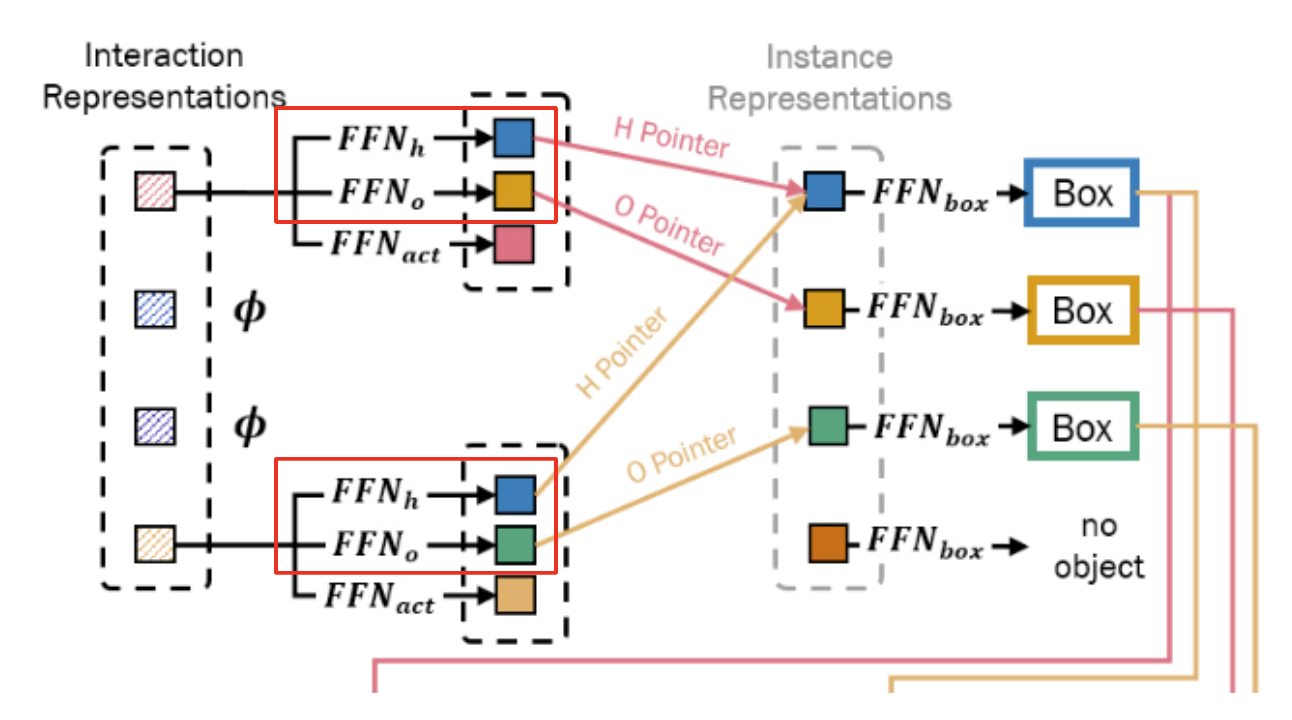
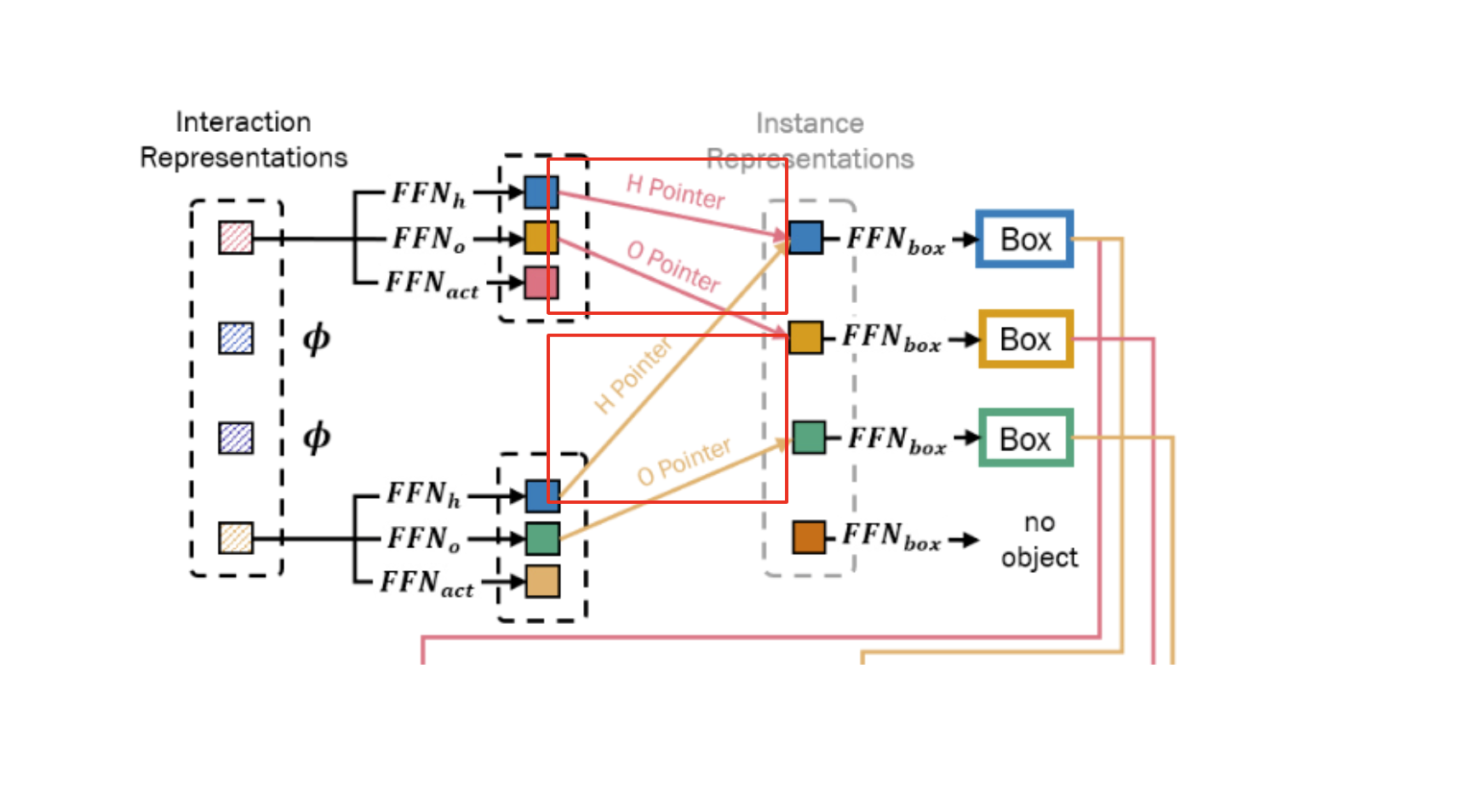
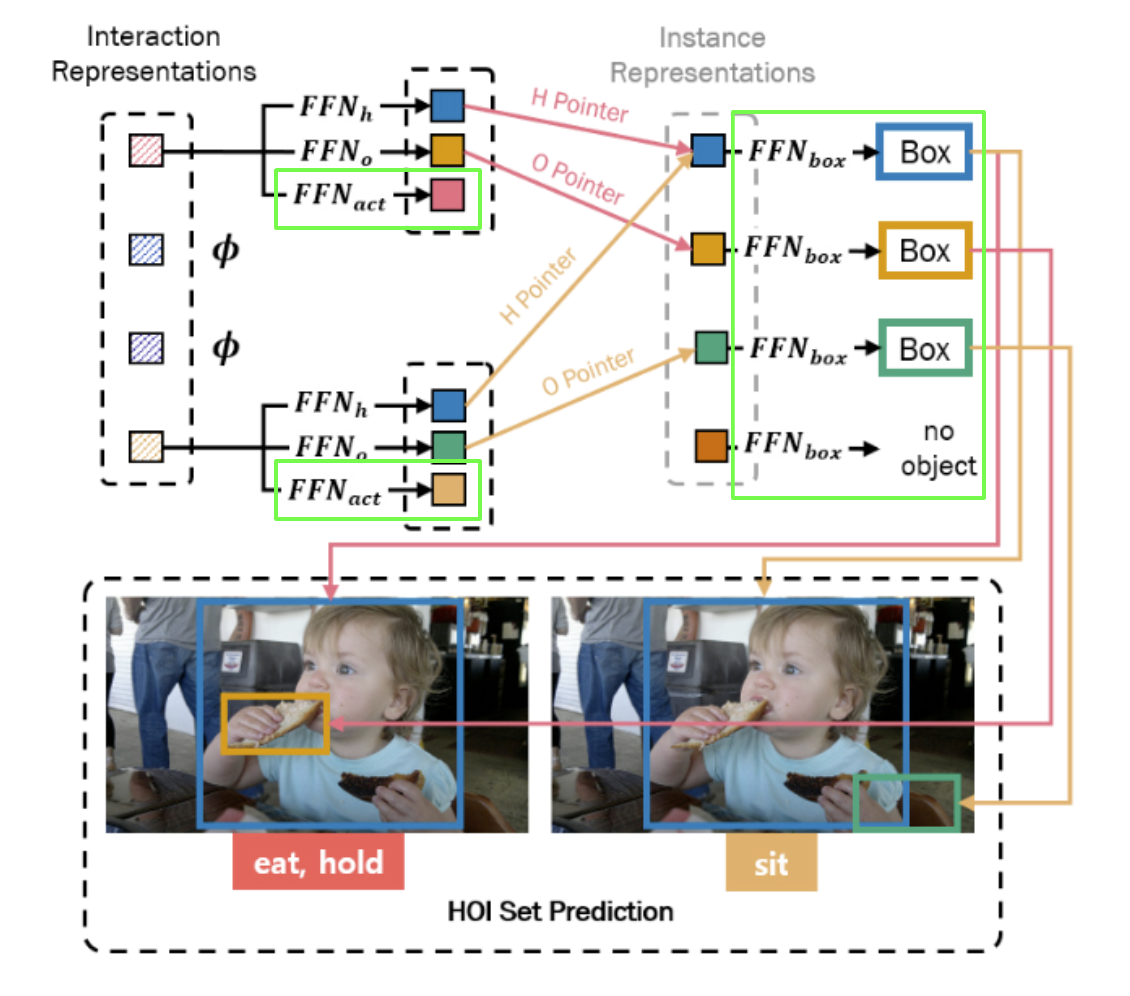
Then, the feed-forward networks (FFNs) are applied to the interaction representation, obtaining a Human Pointer, an Object Pointer, and interaction type. An interesting part of this paper is that the interaction representation (not the instance representation!) “localizes” humand and object regions by pointing the corresponding instance representations using the Human Pointer and Object Pointer (HO Pointer). This approach avoids direct bounding box regression which incurs a problem when an object(a cup of coffee) involves in multiple interactions(multiple humans or different behaviors such as holding or pushing).
In simple words, HO Pointer “associates” instance and interaction representations. This approach enables more efficient learning of localization without needing to learn localization redundantly for every interaction.
Now, let’s look at the heart of HOTR: HO Pointers
HO Pointers
As mentioned earlier, feed-forward networks are applied to the interaction representation and obtain a Human Pointer, an Object Pointer, and interaction type. HO Pointers (i.e., Human and Object Pointer) contain the indices of the corresponding instance representations of the interacting human and object. Let’s take a deeper look at a more formal description.
[1] The interaction decoder transforms \(K\) interaction queries to \(K\) interaction representations
[2] Then, each interaction representation \(z_i\) is fed into two feed-forward networks:
\[FFN_h : \mathbb{R}^d \rightarrow \mathbb{R}^d\] \[FFN_o : \mathbb{R}^d \rightarrow \mathbb{R}^d\]to obtain vectors \(v_i^h\) and \(v_i^o\)
\[v_i^h = FFN_h(z_i)\] \[v_i^o = FFN_o(z_i)\][3] Finally, the Human Pointer and Object Pointer \(\hat{c}_i^h\) and \(\hat{c}_i^o\) which are the indices of the instance representations with the highest similarity scores are obtained by
\[\hat{c}\_i^h = \underset{j}{argmax}(sim(v_i^h, \mu_j))\] \[\hat{c}\_i^o = \underset{j}{argmax}(sim(v_i^o, \mu_j))\]where \(\mu_j\) is the \(j-th\) instance representation and \(sim(u,v) = \frac{u^Tv}{\lVert u \rVert \lVert v \rVert}\)
Recomposition for HOI Set Prediction
We’ve now obtained the following:
\(N\) instance presentations \(\mu\)
\(K\) interaction representations \(z\) and their HO Pointers \(\hat{c}^h\) and \(\hat{c}^o\)
With \(\gamma\) interaction classes, we recompose by applying the feed-forward networks for bounding box regression and action classification as
\[FFN\_{box}: \mathbb{R}^d \rightarrow \mathbb{R} \rightarrow \mathbb{R}^4\] \[FFN\_{act}: \mathbb{R}^d \rightarrow \mathbb{R}^{\gamma}\]Then, the final HOI prediction for the \(i-th\) interaction representation \(z_i\) is
\[\hat{b}\_i^h = FFN\_{box}(\mu\_{\hat{c}\_i^h}) \in \mathbb{R}^4\] \[\hat{b}\_i^o = FFN\_{box}(\mu\_{\hat{c}\_i^o}) \in \mathbb{R}^4\] \[\hat{a}\_i = FFN\_{act}(z_i) \in \mathbb{R}^{\gamma}\]Hence, we now obtained the set of \(K\) HOI triplets:
\[\text{HOI triplets}= \{ \langle \hat{b}\_i^h, \hat{b}\_i^o, \hat{a}\_i \rangle \}\_{i=1}^K\]Complexity & Inference time
Previous parallel HOI detectors reduce inference time with a fast matching of triplets based on simple heuristics such as distances or IoU.
HOTR further reduces the inference time (after object detection) by associating \(K\) interactions with \(N\) instances. Hence, the time complexity is \(o(KN)\).
Also, HOTR doesn’t require the expensive post-processing steps such as NMS for the interaction region and triplet matching. HOTR reduces the inference time by \(4 \sim 8ms\) but still shows performance gains.
Hungarian Matching for HOI Detection
HOTR predicts \(K\) HOI triplets: human box, object box, and binary classification for \(a\) types of interactions. Thus, each prediction captures a unique \(\langle human, object \rangle\) pair with one or more interactions.
\(K\) is set to be larger than the intuitive number of interacting pairs in an image.
Let \(\mathcal{Y}\) denote the set of GT HOI tripltes and \(\hat{\mathcal{Y}}=\{ \hat{y}_i \}\_{i=1}^K\) as the set of \(K\) predictions.
We consider \(\mathcal{Y}\) as a set of size \(K\) with padding of \(\emptyset\) for no interaction as \(K\) is larger than the number of unique interacting pairs.
Then, we search for a permutation of \(K\) elements \(\sigma \in \mathfrak{S}_K\) to find a bipartiate matching with the lowest cost :
\[\hat{\sigma} = \underset{\sigma \in \mathfrak{S}\_K}{argmin} \sum_i^K C\_{match}(y_i, \hat{y}\_{\sigma(i)})\]where \(C\_{match}\) is a pair-wise matching cose between GT \(y_i\) and a prediction with index \(\sigma(i)\).
But the ground truth label \(y_i\) is in the form of \(\langle hbox, obox, action \rangle\) while \(\hat{y}\_{\sigma(i)}\) is in the form of \(\langle hidx, oidx, action \rangle\) while \(h\) and \(o\) denote human and object. Thus, we need to modify the cost function to correctly compute the cost.
Let \(\Phi\) be a mapping function from GT label \(\langle hidx, oidx \rangle\) to GT label \(\langle hbox, obox \rangle\) by optimal assignment for object detection
\[\Phi: idx \rightarrow box\]By inversing the mapping function,
\[\Phi^{-1}: box \rightarrow idx\]we get the GT idx from the GT box.
Then, let \(M \in \mathbb{R}^{d \times N}\) be a set of normalized instance representations \(\mu' = \frac{\mu}{\lVert \mu \rVert} \in \mathbb{R}^d\), i.e., \(M = [\mu'_1 \cdots \mu'_N]\).
We compute \(\hat{P}^h \in \mathbb{R}^{K \times N}\) which is the set of softmax predictions for the H Pointer (represent the index for instance representation):
\[\hat{P}^h = \Vert\_{i=1}^K softmax((\bar{v_i}^h)^T M)\]where \(\Vert_{i=1}^K\) denotes the vertical stack of the row vectors and \(\bar{v}_i^h = v_i^ / \lVert v_i^h \rVert\). \(\hat{P}^o\) is defined simiarly.
Now, given the GT \(y_i = (b_i^h, b_i^o, a_i)\), \(\hat{P}^h\) and \(\hat{P}^o\), we convert the GT box to indices by
\[c_i^h = \Phi^{-1}(b_i^h)\] \[c_i^o = \Phi^{-1}(b_i^o)\]and compute the matching cost function:
\[C\*{match}(y\*i, \hat{y}\_{\sigma(i)}) = -\alpha \cdot \mathbb{1}\_{\{a_i \neq \emptyset \}} \hat{P}^h[\sigma(i), c_i^h]\] \[-\beta \cdot \mathbb{1}\_{\{a_i \neq \emptyset \}} \hat{P}^o[\sigma(i), c_i^o]\] \[+\mathbb{1}\_{\{a_i \neq \emptyset \}} \mathcal{L}\_{act}[a_i, \hat{a}\_{\sigma(i)}]\]where \(\hat{P}[i,j]\) denotes the element at \(i-th\) row and \(j-th\) column, and \(\hat{a}\_{\sigma(i)}\) is the predicted action.
The action matching cost is computed as
\[\mathcal{L}\_{act}(a_i, \hat{a}\_{\sigma(i)}) = BCELoss(a_i,\hat{a}\_{\sigma(i)})\]Final Set Prediction Loss for HOTR
Now we compute the Hungarian loss for all pairs matched above.
The loss for the HOI triplets involve the localization loss and classification loss
\[\mathcal{L}\_H = \sum\_{i=1}^K[\mathcal{L}\_{loc}(c_i^h, c_i^o, z\_{\sigma(i)}) + \mathcal{L}\_{act}(a_i, \hat{a}\_{\sigma(i)})]\]where the localization loss \(\mathcal{L}\_{loc}(c_i^h, c_i^o, z\_{\sigma(i)})\) is denoted as
\[\mathcal{L}\_{loc} = -\log \frac{exp(sim(FFN*h(z\_{\sigma(i)}), \mu\_{c_i^h} ) / \tau)}{\sum\_{k=1}^N exp(sim(FFN_h(z\_{\sigma(i)}), \mu_k ) / \tau)} -\log \frac{exp(sim(FFN_o(z\_{\sigma(i)}), \mu*{c_i^o} ) / \tau)}{\sum\_{k=1}^N exp(sim(FFN_o(z\_{\sigma(i)}), \mu_k ) / \tau)}\]where \(\tau\) is the temperature controling the smoothness of the loss function. \(\tau=0.1\) is used in the paper.
Defining No-Interaction with HOTR
HOI utilizes multi-label classification for action classification and each action is treated as an individual binary classification. Therefore, there’s no explicit no-interaction label like in DETR which could suppress the probability of other classes. Hence, HOTR sets an explicit class that learns the interactiveness (1 if there’s any interaction between the pair, 0 otherwise) and suppresses the predictions for reundant pairs with a low interactiveness score. The low interactiveness score is defined as No-Interaction class.
Experiments
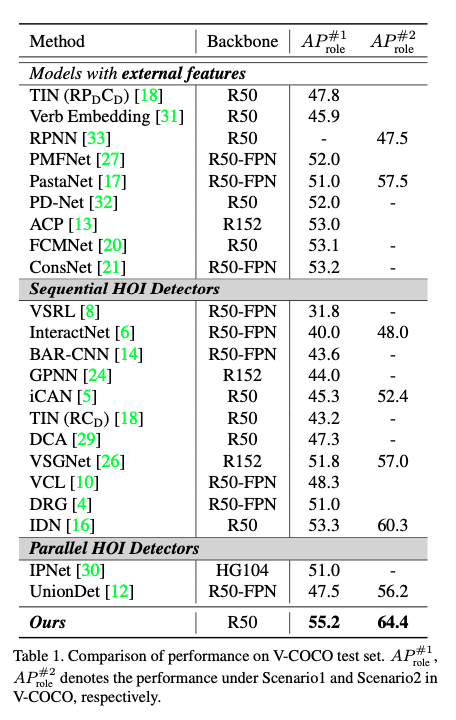
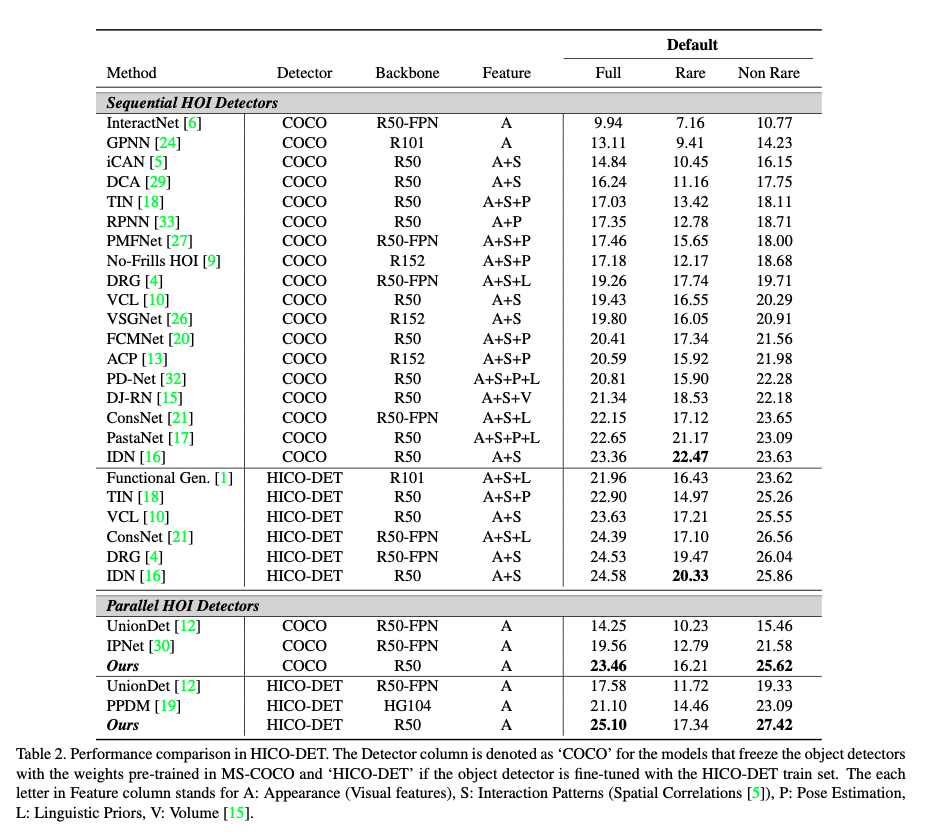
HOTR was tested on the V-COCO and HICO-DET dataset. Below are the performance details
Conclusion
Understanding visual perceptions is one of the most crucial task in computer vision. Human-Object Interaction (HOI) detection is a more advanced task than plain object detection task, understanding interactions between the subject of the interaction (human) and the objects in the scene. HOTR introduces a novel transformer encoder-decoder architecture which greatly reduce inference time with various methods including HO Pointer.
References
[1] https://arxiv.org/abs/2104.13682
[2] https://www.youtube.com/watch?v=hmfRkkmt0WE